已知方程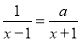 的解为x=2,求
的解为x=2,求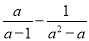 的值.
的值.
 , .
【解析】试题分析:根据分式方程的解为x=2,代入到分式方程,求出a的值,把通分化简,再把a的值代入计算即可求出代数式的值.
把x=2代入得,a=3,
∴原式=﹣
=
=,
当a=3时,原式==.
, .
【解析】试题分析:根据分式方程的解为x=2,代入到分式方程,求出a的值,把通分化简,再把a的值代入计算即可求出代数式的值.
把x=2代入得,a=3,
∴原式=﹣
=
=,
当a=3时,原式==. 2cos30°的值等于
(A)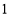 (B)
(B) (C)
(C) (D)
(D)
 D.
【解析】
试题分析:根据特殊角的三角函数值直接解答即可.
试题解析:2cos30°=2×.
故选D.
D.
【解析】
试题分析:根据特殊角的三角函数值直接解答即可.
试题解析:2cos30°=2×.
故选D. 如图,在△ABC中,已知∠C=90°,AC=4,BC=3,那么下列结论不正确的是( )
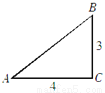
A. sinA=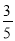 B. cosA=
B. cosA=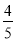 C. tanA=
C. tanA=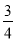 D. cosB=
D. cosB=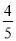
 D
【解析】∵∠C=90°,AC=4,BC=3,∴AB==5,
∴sinA==,cosA== , tanA== , cosB==,
故选D.
D
【解析】∵∠C=90°,AC=4,BC=3,∴AB==5,
∴sinA==,cosA== , tanA== , cosB==,
故选D. 如图,在△ABC中,∠C=90°,AB=13,BC=5,则sin A的值是( )

A. 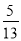 B.
B. 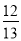 C.
C. 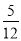 D.
D. 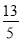
 A
【解析】【解析】
在Rt△ABC中,由勾股定理得,BC==12,∴sinA=,故选B.
A
【解析】【解析】
在Rt△ABC中,由勾股定理得,BC==12,∴sinA=,故选B. 在△ABC中,已知AC=3,BC=4,AB=5,那么下列结论正确的是( )
A.sinA=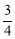 B.cosA=
B.cosA=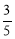 C.tanA=
C.tanA=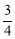 D.cosB=
D.cosB=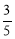
 B
【解析】
试题分析:先根据勾股定理的逆定理判断△ABC的形状,再根据三角函数的定义依次分析各项即可.
∵
∴△ABC是直角三角形
∴,,,
故选B.
B
【解析】
试题分析:先根据勾股定理的逆定理判断△ABC的形状,再根据三角函数的定义依次分析各项即可.
∵
∴△ABC是直角三角形
∴,,,
故选B. 在△ABC中,若cosA=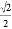 ,tanB=
,tanB=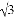 ,则这个三角形一定是( )
,则这个三角形一定是( )
A. 锐角三角形 B. 直角三角形 C. 钝角三角形 D. 等腰三角形
 A
【解析】试题解析:∵cosA=,tanB=,
∴∠A=45°,∠B=60°.
∴∠C=180°-45°-60°=75°.
∴△ABC为锐角三角形.
故选A.
A
【解析】试题解析:∵cosA=,tanB=,
∴∠A=45°,∠B=60°.
∴∠C=180°-45°-60°=75°.
∴△ABC为锐角三角形.
故选A. 某人沿倾斜角为β的斜坡前进100m,则他上升的最大高度是( )m
A.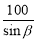 B.
B.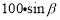 C.
C.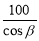 D.
D.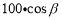
 B
【解析】
试题分析:设他上升的最大高度是hm,根据坡角及三角函数的定义即可求得结果.
设他上升的最大高度是hm,由题意得
,解得
故选B.
B
【解析】
试题分析:设他上升的最大高度是hm,根据坡角及三角函数的定义即可求得结果.
设他上升的最大高度是hm,由题意得
,解得
故选B. 如图所示,△ABC是不等边三角形,DE=BC,以D、E为两个顶点作位置不同的三角形,使所作三角形与△ABC全等,这样的三角形最多可以画出( )个.
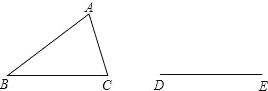
A.2 B.4 C.6 D.8
 B.
【解析】
试题分析:可以做4个,分别是以D为圆心,AB为半径,作圆,以E为圆心,AC为半径,作圆.两圆相交于两点(D,E上下各一个),经过连接后可得到两个.然后以D为圆心,AC为半径,作圆,以E为圆心,AB为半径,作圆.两圆相交于两点(D,E上下各一个),经过连接后可得到两个.如图.
故选:B.
B.
【解析】
试题分析:可以做4个,分别是以D为圆心,AB为半径,作圆,以E为圆心,AC为半径,作圆.两圆相交于两点(D,E上下各一个),经过连接后可得到两个.然后以D为圆心,AC为半径,作圆,以E为圆心,AB为半径,作圆.两圆相交于两点(D,E上下各一个),经过连接后可得到两个.如图.
故选:B. 如图所示,P是正方形ABCD内一点,将△ABP绕点B顺时针方向旋转能与△CBP′重合,若PB=2,则PP′=_______.

 【解析】【解析】
∵四边形ABCD为正方形,∴∠ABC=90°.∵△ABP绕点B顺时针方向旋转能与△CBP′重合,∴∠PBP′=∠ABC=90°,PB=P′B=2,∴△PBP′为等腰直角三角形,∴PP′=PB=.
故答案为: .
【解析】【解析】
∵四边形ABCD为正方形,∴∠ABC=90°.∵△ABP绕点B顺时针方向旋转能与△CBP′重合,∴∠PBP′=∠ABC=90°,PB=P′B=2,∴△PBP′为等腰直角三角形,∴PP′=PB=.
故答案为: . 某产品的标志图案如图(1)所示,要在所给的图3-122(2)中,把A,B,C三个菱形通过一种或几种变换,使之变为与图(1)一样的图案.
(1)请你在图3-122(2)中作出变换后的图案;(最终图案用实线)
(2)你所用的变换方法是_________.(填序号)
①将菱形B向上平移;②将菱形B绕点O顺时针旋转120°;③将菱形B绕点O旋转180.
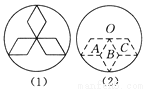
 ①或③
【解析】试题分析:首先分析①②的不同,变化前后,AC的位置不变,只有B的位置由O的下方变为O的上方,据此即可作出判断.
试题解析:【解析】
(1)观察分析①②的不同,变化前后,AC的位置不变,而B的位置由O的下方变为O的上方,进而可得两者对应点的连线交于点O,即进行了中心对称变化,变换方法是将菱形B绕点O旋转180°,可作图得:
(2)变换方法是将菱形B绕点O旋转180...
①或③
【解析】试题分析:首先分析①②的不同,变化前后,AC的位置不变,只有B的位置由O的下方变为O的上方,据此即可作出判断.
试题解析:【解析】
(1)观察分析①②的不同,变化前后,AC的位置不变,而B的位置由O的下方变为O的上方,进而可得两者对应点的连线交于点O,即进行了中心对称变化,变换方法是将菱形B绕点O旋转180°,可作图得:
(2)变换方法是将菱形B绕点O旋转180...