题目内容
在△ABC中,若cosA=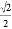 ,tanB=
,tanB=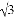 ,则这个三角形一定是( )
,则这个三角形一定是( )
A. 锐角三角形 B. 直角三角形 C. 钝角三角形 D. 等腰三角形
 A
【解析】试题解析:∵cosA=,tanB=,
∴∠A=45°,∠B=60°.
∴∠C=180°-45°-60°=75°.
∴△ABC为锐角三角形.
故选A.
A
【解析】试题解析:∵cosA=,tanB=,
∴∠A=45°,∠B=60°.
∴∠C=180°-45°-60°=75°.
∴△ABC为锐角三角形.
故选A.
练习册系列答案
 优等生题库系列答案
优等生题库系列答案 53天天练系列答案
53天天练系列答案
相关题目
不等式3x<6的解集是_____;使该不等式成立的正整数解是___,当_____时,不等式3x>7不成立.
 x<2 1 x≤
【解析】3x<6的解集为x<2;
其正整数解为1,
当x≤时,不等式3x>7不成立.
故答案为(1). x<2 (2). 1 (3). x≤
x<2 1 x≤
【解析】3x<6的解集为x<2;
其正整数解为1,
当x≤时,不等式3x>7不成立.
故答案为(1). x<2 (2). 1 (3). x≤ 如图,AD是△ABC的角平分线,DE⊥AB于E,DF⊥AC于F,直线AD交EF于点O.问直线AD是线段EF的垂直平分线吗?请说明理由.
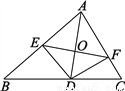
 AD是线段EF的垂直平分线,理由见解析
【解析】试题分析:由AD为△ABC的角平分线,得到DE=DF,推出∠AEF和∠AFE相等,得到AE=AF,即可推出结论.
试题解析:∵AD为△ABC的角平分线,DE⊥AB,DF⊥AC,
∴DE=DF,∠AED=∠AFD=90°,
∴∠DEF=∠DFE,
∴∠AEF=∠AFE,
∴AE=AF,
∴点A、D都在EF的垂直...
AD是线段EF的垂直平分线,理由见解析
【解析】试题分析:由AD为△ABC的角平分线,得到DE=DF,推出∠AEF和∠AFE相等,得到AE=AF,即可推出结论.
试题解析:∵AD为△ABC的角平分线,DE⊥AB,DF⊥AC,
∴DE=DF,∠AED=∠AFD=90°,
∴∠DEF=∠DFE,
∴∠AEF=∠AFE,
∴AE=AF,
∴点A、D都在EF的垂直... 请充分发挥你的想象力,任选其一完成下面的设计
(1)以一直角三角形为“基本图形”,利用旋转而得到一个风车或风轮图案.你能设计出几种风车风轮图案呢?请将你的图案画出来,完成后与同学进行交流.
(2)利用圆、三角形、正六边形,通过平移或旋转来设计一个图案,完成后与同学交流你的作品,说明你的设计意图.
 见解析
【解析】试题分析:根据旋转的角度不同可得到不同的风车形状,只要满足题意即可.
试题解析:【解析】
选(1),所画的是旋转90°的情况.
见解析
【解析】试题分析:根据旋转的角度不同可得到不同的风车形状,只要满足题意即可.
试题解析:【解析】
选(1),所画的是旋转90°的情况. 将点A绕另一个点O旋转一周,点A在旋转过程中所经过的路线是_______.
 圆
【解析】
试题分析:根据圆的定义,到定点的距离等于定长的点的轨迹是圆.
依题意,点A绕点O旋转一周的路线是圆.
圆
【解析】
试题分析:根据圆的定义,到定点的距离等于定长的点的轨迹是圆.
依题意,点A绕点O旋转一周的路线是圆. 已知方程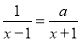 的解为x=2,求
的解为x=2,求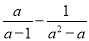 的值.
的值.
 , .
【解析】试题分析:根据分式方程的解为x=2,代入到分式方程,求出a的值,把通分化简,再把a的值代入计算即可求出代数式的值.
把x=2代入得,a=3,
∴原式=﹣
=
=,
当a=3时,原式==.
, .
【解析】试题分析:根据分式方程的解为x=2,代入到分式方程,求出a的值,把通分化简,再把a的值代入计算即可求出代数式的值.
把x=2代入得,a=3,
∴原式=﹣
=
=,
当a=3时,原式==. 若关于x的方程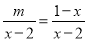 有增根,则m的值为( )
有增根,则m的值为( )
A. 0 B. 1 C. -1 D. 2
 C
【解析】试题解析:方程两边同乘以x?2,得
①
∵原方程有增根,
∴x?2=0,
即x=2.
把x=2代入①,得
m=?1.
故选C.
C
【解析】试题解析:方程两边同乘以x?2,得
①
∵原方程有增根,
∴x?2=0,
即x=2.
把x=2代入①,得
m=?1.
故选C. 在△ABC中,∠C=90°,AB=13,BC=5,则tanB=________.
 【解析】∵∠C=90°,AB=13,BC=5,∴AC==12,∴tanB=,
故答案为: .
【解析】∵∠C=90°,AB=13,BC=5,∴AC==12,∴tanB=,
故答案为: . 如图,在Rt△ABC中,∠ACB=90°,D是AB上一点,且∠ACD=∠B;求证:CD⊥AB;
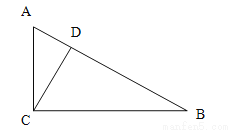
 证明过程见解析
【解析】试题分析:根据∠ACB=90°得出∠A+∠B=90°,结合已知条件得出∠A+∠ACD=90°,从而得出答案.
试题解析:∵∠ACB=90° ∴∠A+∠B=90° ∵∠ACD=∠B ∴∠A+∠ACD=90° ∴∠ADC=90°
∴CD⊥AB
证明过程见解析
【解析】试题分析:根据∠ACB=90°得出∠A+∠B=90°,结合已知条件得出∠A+∠ACD=90°,从而得出答案.
试题解析:∵∠ACB=90° ∴∠A+∠B=90° ∵∠ACD=∠B ∴∠A+∠ACD=90° ∴∠ADC=90°
∴CD⊥AB 
