题目内容
如图,在△ABC中,∠C=90°,AB=13,BC=5,则sin A的值是( )

A. 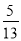 B.
B. 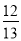 C.
C. 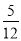 D.
D. 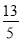
 A
【解析】【解析】
在Rt△ABC中,由勾股定理得,BC==12,∴sinA=,故选B.
A
【解析】【解析】
在Rt△ABC中,由勾股定理得,BC==12,∴sinA=,故选B.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
不等式x-3>1的解集是( )
A. x>2 B. x>4 C. x>-2 D. x>-4
 B
【解析】试题分析:根据不等式的基本性质即可得到结果.
x-3>1
x>4
故选B.
B
【解析】试题分析:根据不等式的基本性质即可得到结果.
x-3>1
x>4
故选B. 如图,在△ABC中,AB=AD=DC,∠BAD=26°.求∠B和∠C的度数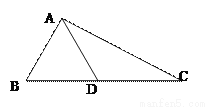
 77° 38.5°
【解析】【解析】
∵ AB=AD,
∴∠B=∠ADB. ……………… 2分
∵在△ABD中,∠B+∠ADB+∠BAD=180°,∠BAD=26°,
∴∠B=∠ADB=77°. ……………… 4分
∵AD.=DC,
∴∠DAC =∠C. ……………… 6分
∵∠ADB=∠DAC+∠C, ……………… 7分
∴∠ADB=2∠C,
...
77° 38.5°
【解析】【解析】
∵ AB=AD,
∴∠B=∠ADB. ……………… 2分
∵在△ABD中,∠B+∠ADB+∠BAD=180°,∠BAD=26°,
∴∠B=∠ADB=77°. ……………… 4分
∵AD.=DC,
∴∠DAC =∠C. ……………… 6分
∵∠ADB=∠DAC+∠C, ……………… 7分
∴∠ADB=2∠C,
... 你能用一张长方形的纸片折出一个正三角形吗?动手试一试,简单叙述你的折法.
 如图,先把矩形纸片对折,然后在沿着BM对折使C落在EF上的N点,再折出BM和CN即可.
【解析】试题分析:把长方形纸片ABCD的宽对折,然后展开,折痕记为EF,再把AD边折起,点D折叠到EF上,与EF的重合点为M,在CD上的折痕为点G,再沿GM对折,在AB上的折痕为H,则三角形AHG就是一个正三角形.
试题解析:【解析】
如图,
连接AM,在△AMG和△AMH中,
AM=...
如图,先把矩形纸片对折,然后在沿着BM对折使C落在EF上的N点,再折出BM和CN即可.
【解析】试题分析:把长方形纸片ABCD的宽对折,然后展开,折痕记为EF,再把AD边折起,点D折叠到EF上,与EF的重合点为M,在CD上的折痕为点G,再沿GM对折,在AB上的折痕为H,则三角形AHG就是一个正三角形.
试题解析:【解析】
如图,
连接AM,在△AMG和△AMH中,
AM=... 如图所示,P是正方形ABCD内一点,将△ABP绕点B顺时针方向旋转能与△CBP′重合,若PB=2,则PP′=_______.

 【解析】【解析】
∵四边形ABCD为正方形,∴∠ABC=90°.∵△ABP绕点B顺时针方向旋转能与△CBP′重合,∴∠PBP′=∠ABC=90°,PB=P′B=2,∴△PBP′为等腰直角三角形,∴PP′=PB=.
故答案为: .
【解析】【解析】
∵四边形ABCD为正方形,∴∠ABC=90°.∵△ABP绕点B顺时针方向旋转能与△CBP′重合,∴∠PBP′=∠ABC=90°,PB=P′B=2,∴△PBP′为等腰直角三角形,∴PP′=PB=.
故答案为: . 解方程:
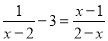
 x=3
【解析】试题分析:按照解分式方程的步骤解方程即可.
试题解析:去分母,得
去括号,得
移项,得
合并同类项,得
系数化为1,得
检验:当时,
是原方程的解.
x=3
【解析】试题分析:按照解分式方程的步骤解方程即可.
试题解析:去分母,得
去括号,得
移项,得
合并同类项,得
系数化为1,得
检验:当时,
是原方程的解. 分式方程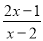 =1的解为( )
=1的解为( )
A. x=﹣1 B. x=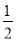 C. x=1 D. x=2
C. x=1 D. x=2
 A
【解析】【解析】
去分母得:2x﹣1=x﹣2,
解得:x=﹣1,
经检验x=﹣1是分式方程的解,
则分式方程的解为x=﹣1.
故选:A.
A
【解析】【解析】
去分母得:2x﹣1=x﹣2,
解得:x=﹣1,
经检验x=﹣1是分式方程的解,
则分式方程的解为x=﹣1.
故选:A. 等腰三角形一腰上的高与腰长之比是1?2,则等腰三角形顶角的度数为( )
A. 30° B. 50° C. 60°或120° D. 30°或150°
 D
【解析】如图1,当高BD在三角形的内部时,
∵高BD是腰长AB的一半,
∴sin A=,∴∠A=30°;
如图2,当高CD在三角形的外部时,
∵高CD是腰长AC的一半,
∴sin∠1=,∴∠1=30°,
∴∠BAC=180°-30°=150°,
∴该三角形的顶角的度数是30°或150°,
故选D.
D
【解析】如图1,当高BD在三角形的内部时,
∵高BD是腰长AB的一半,
∴sin A=,∴∠A=30°;
如图2,当高CD在三角形的外部时,
∵高CD是腰长AC的一半,
∴sin∠1=,∴∠1=30°,
∴∠BAC=180°-30°=150°,
∴该三角形的顶角的度数是30°或150°,
故选D. 已知:AB⊥BC,AD⊥DC,∠1=∠2,问:△ABC≌△ADC吗?说明理由.
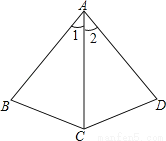
 见解析
【解析】试题分析:根据全等三角形的判定定理AAS进行证明.
试题解析:【解析】
△ABC≌△ADC.理由如下:
∵AB⊥BC,AD⊥DC,∴∠B=∠D=90°.
在△ABC与△ADC中,∵,∴△ABC≌△ADC(AAS).
见解析
【解析】试题分析:根据全等三角形的判定定理AAS进行证明.
试题解析:【解析】
△ABC≌△ADC.理由如下:
∵AB⊥BC,AD⊥DC,∴∠B=∠D=90°.
在△ABC与△ADC中,∵,∴△ABC≌△ADC(AAS). 
