题目内容
已知方程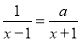 的解为x=2,求
的解为x=2,求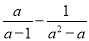 的值.
的值.
 , .
【解析】试题分析:根据分式方程的解为x=2,代入到分式方程,求出a的值,把通分化简,再把a的值代入计算即可求出代数式的值.
把x=2代入得,a=3,
∴原式=﹣
=
=,
当a=3时,原式==.
, .
【解析】试题分析:根据分式方程的解为x=2,代入到分式方程,求出a的值,把通分化简,再把a的值代入计算即可求出代数式的值.
把x=2代入得,a=3,
∴原式=﹣
=
=,
当a=3时,原式==.
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
下列各式分别在什么条件下成立?
(1)a>-a; (2)a2>a; (3)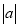 >a.
>a.
 (1)a>0;(2)a>l或a<0;(3)a<0.
【解析】分析:根据不等式的基本性质进行判断即可.
本题解析:
(1)在不等式a>-a的两边同时加上a,得到2a>0,再在不等式的两边同时除以2,得到a>0,即当a>0时,不等式a>-a成立;
(2)在不等式a2>a的两边同时减去a,得到a(a-1)>0,所以
或,
解得a>l或a<0.
即当a>l或a<0时,不等式a2>...
(1)a>0;(2)a>l或a<0;(3)a<0.
【解析】分析:根据不等式的基本性质进行判断即可.
本题解析:
(1)在不等式a>-a的两边同时加上a,得到2a>0,再在不等式的两边同时除以2,得到a>0,即当a>0时,不等式a>-a成立;
(2)在不等式a2>a的两边同时减去a,得到a(a-1)>0,所以
或,
解得a>l或a<0.
即当a>l或a<0时,不等式a2>... 如图,已知△ABC是等边三角形,点B、C、D、E在同一直线上,且CG=CD,DF=DE,则∠E=______。
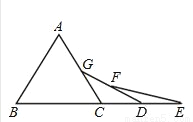
 15°
【解析】试题分析:设∠E=x,根据等边对等角的性质以及三角形的一个外角等于与它不相邻的两个内角的和列式计算即可得解.
【解析】
设∠E=x,
∵DF=DE,
∴∠DFE=∠E=x,
∴∠CDG=∠E+∠DFE=2x,
∵CG=CD,
∴∠CDG=∠CGD=2x,
∴∠ACB=∠CDG+∠CGD=2x+2x=4x,
∵∠ACB=70°,...
15°
【解析】试题分析:设∠E=x,根据等边对等角的性质以及三角形的一个外角等于与它不相邻的两个内角的和列式计算即可得解.
【解析】
设∠E=x,
∵DF=DE,
∴∠DFE=∠E=x,
∴∠CDG=∠E+∠DFE=2x,
∵CG=CD,
∴∠CDG=∠CGD=2x,
∴∠ACB=∠CDG+∠CGD=2x+2x=4x,
∵∠ACB=70°,... 老师拿出6根小木棒,3根长的相同,3根短的也相同,且长的是短的的长度的2倍,请用这6根木棒摆成四个完全相同的三角形.
 见解析
【解析】试题分析:用3根长的构成一个大等边三角形,3根短的构成一个小等边三角形即可.
试题解析:【解析】
如图.
见解析
【解析】试题分析:用3根长的构成一个大等边三角形,3根短的构成一个小等边三角形即可.
试题解析:【解析】
如图. 在△ABC中,若cosA=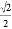 ,tanB=
,tanB=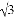 ,则这个三角形一定是( )
,则这个三角形一定是( )
A. 锐角三角形 B. 直角三角形 C. 钝角三角形 D. 等腰三角形
 A
【解析】试题解析:∵cosA=,tanB=,
∴∠A=45°,∠B=60°.
∴∠C=180°-45°-60°=75°.
∴△ABC为锐角三角形.
故选A.
A
【解析】试题解析:∵cosA=,tanB=,
∴∠A=45°,∠B=60°.
∴∠C=180°-45°-60°=75°.
∴△ABC为锐角三角形.
故选A. 分式方程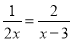 的解是_____.
的解是_____.
 x=﹣1
【解析】试题分析:根据解分式方程的方法可以求得分式方程的解,记住最后要进行检验,本题得以解决.
【解析】
方程两边同乘以2x(x﹣3),得
x﹣3=4x
解得,x=﹣1,
检验:当x=﹣1时,2x(x﹣3)≠0,
故原分式方程的解是x=﹣1,
故答案为:x=﹣1.
x=﹣1
【解析】试题分析:根据解分式方程的方法可以求得分式方程的解,记住最后要进行检验,本题得以解决.
【解析】
方程两边同乘以2x(x﹣3),得
x﹣3=4x
解得,x=﹣1,
检验:当x=﹣1时,2x(x﹣3)≠0,
故原分式方程的解是x=﹣1,
故答案为:x=﹣1. 小红家的阳台上放置了一个晒衣架(如图①),图②是晒衣架的侧面示意图,立杆AB,CD相交于点O,B,D两点立于地面,经测量:AB=CD=136 cm,OA=OC=51 cm,OE=OF=34 cm,现将晒衣架完全稳固张开,扣链EF成一条线段,且EF=32 cm(参考数据:sin 61.9°≈0.882,cos 61.9°≈0.471,tan 28.1°≈0.534).

(1)求证:AC∥BD.
(2)求扣链EF与立杆AB的夹角∠OEF的度数(结果精确到0.1°).
(3)小红的连衣裙穿在晒衣架上的总长度达到122 cm,垂挂在晒衣架上是否会拖落到地面?请通过计算说明理由.
 (1)见解析;(2)61.9°;(3)会拖落到地面.
【解析】试题解析
(1)证明:证法一: 相交于点 ,
同理可证:
证法二:
∴
又
(2)【解析】
在中, 作于点,
则
用计算器求得
(3)解法一:小红的连衣裙会拖落到地面;
在中,
过点 作于点,
同可证:
则
∴所以:小红的连衣裙垂挂在衣架后的总...
(1)见解析;(2)61.9°;(3)会拖落到地面.
【解析】试题解析
(1)证明:证法一: 相交于点 ,
同理可证:
证法二:
∴
又
(2)【解析】
在中, 作于点,
则
用计算器求得
(3)解法一:小红的连衣裙会拖落到地面;
在中,
过点 作于点,
同可证:
则
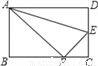
∴所以:小红的连衣裙垂挂在衣架后的总... 如图,沿AE折叠矩形纸片ABCD,使点D落在BC边的点F处已知AB=8,BC=10,则tan∠EFC的值为( )
A. 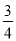 B.
B. 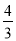 C.
C. 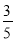 D.
D. 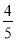
 A
【解析】试题解析:根据题意可得:在Rt△ABF中,有AB=8,AF=AD=10,BF=6,
而Rt△ABF∽Rt△EFC,故有∠EFC=∠BAF,故tan∠EFC=tan∠BAF=.
故选A.
A
【解析】试题解析:根据题意可得:在Rt△ABF中,有AB=8,AF=AD=10,BF=6,
而Rt△ABF∽Rt△EFC,故有∠EFC=∠BAF,故tan∠EFC=tan∠BAF=.
故选A. 在一个直角三角形中,有一个锐角等于30°,则另一个锐角的大小为______度.
 60
【解析】【解析】
∵三角形是直角三角形,一个锐角等于30°,∴另一个锐角为90°﹣30°=60°.
故答案为:60.
60
【解析】【解析】
∵三角形是直角三角形,一个锐角等于30°,∴另一个锐角为90°﹣30°=60°.
故答案为:60. 
