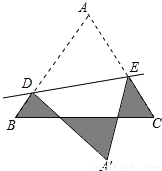
如图，等边△ABC的边长为1cm，D、E分别是AB、AC上的点，将△ADE沿直线DE折叠，点A落在点A′处，且点A′在△ABC外部，则阴影部分图形的周长为_______cm．
3
【解析】因为等边三角形ABC的边长为1cm，
所以AB=BC=AC=1cm，
因为△ADE沿直线DE折叠，点A落在点F处，
所以AD=FD，AE=FE，
所以阴影部分图形的周长为：
BD+FD+BC+FE+EC=BD+AD+BC+AE+EC=AB+BC+AC=1+1+1=3(cm)
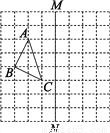
故答案为：3. 如图，在正方形网格上有一个△ABC.
(1)作△ABC关于直线MN的对称图形(不写作法)；
(2)在网格上的最小正方形的边长为1，求△ABC的面积．
(1)见解析;（2）
【解析】试题分析：（1）根据网格特点分别找到A、B、C关于直线MN对称的点，然后顺次连接即可得；
（2）用三角形ABC所在长方形的面积减去四周三个小三角形的面积即可得.
试题解析：（1）如图所示：
（2）S△ABC＝2×3－2×(×1×2)－×1×3＝. 如图，在△ABC中，AB=AD=DC，∠BAD=26°.求∠B和∠C的度数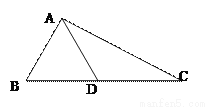
77° 38.5°
【解析】【解析】
∵ AB＝AD，
∴∠B＝∠ADB． ……………… 2分
∵在△ABD中，∠B+∠ADB+∠BAD＝180°，∠BAD＝26°，
∴∠B＝∠ADB＝77°． ……………… 4分
∵AD.＝DC，
∴∠DAC ＝∠C． ……………… 6分
∵∠ADB＝∠DAC+∠C， ……………… 7分
∴∠ADB＝2∠C，
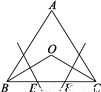
... 如图，在等边三角形ABC中，∠B、∠C的平分线相交于点O，作BO、CO的垂直平分线分别交BC于点E、F.小明说：“E、F是BC的三等分点．”你同意他的说法吗？请说明理由．
同意，理由见解析
【解析】试题分析：连接OE、OF，根据等边三角形角平分线的性质，可得∠OBC=∠OCB=30°，由BC的垂直平分线，可知BE=OE，∠EBO=∠EOB=30°，∠OEF=60°，再证，∠OFE=60°，得出△OEF为等边三角形，从而可知EF=OE=BE=OF=FC，得出结论．
试题解析：同意．理由如下：
连接OE、OF，
∵E为BO垂直平分线上的点，且∠O... 如图，AD是△ABC的角平分线，DE⊥AB于E，DF⊥AC于F，直线AD交EF于点O.问直线AD是线段EF的垂直平分线吗？请说明理由．
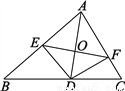
AD是线段EF的垂直平分线，理由见解析
【解析】试题分析：由AD为△ABC的角平分线，得到DE=DF，推出∠AEF和∠AFE相等，得到AE=AF，即可推出结论.
试题解析：∵AD为△ABC的角平分线，DE⊥AB，DF⊥AC，
∴DE=DF，∠AED=∠AFD=90°，
∴∠DEF=∠DFE，
∴∠AEF=∠AFE，
∴AE=AF，
∴点A、D都在EF的垂直... 如图，在等边△ABC中，P为△ABC内任意一点，PD⊥BC于D，PE⊥AC于E，PF⊥AB于F，AM⊥BC于M，试猜想AM、PD、PE、PF之间的关系，并说明你的猜想．
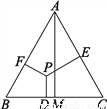
AM＝PD＋PE＋PF，理由见解析
【解析】试题分析：连接AP、BP、CP，根据面积相等，又利用△ABC是等边三角形，即可得PE+PD+PF=AM.
试题解析：PE+PD+PF=AM，理轴如下：
连接AP、BP、CP，
∵S△ABP+S△BCP+S△ACP=S△ABC，
∴AB×PE+BC×PD+AC×PF＝BC×AM，
∵△ABC是等边三角形，
∴AB=... 如图，∠AOB＝30°，角内有一点P，PO＝10cm，两边上各有一点Q，R(均不同于点O)，则△PQR的周长的最小值是多少？
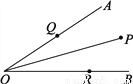
10cm
【解析】试题分析：设点P关于OA的对称点是E，关于OB的对称点是F，当点R、Q在EF上时，△PQR的周长=PQ+QR+PR=EF，此时周长最小．
试题解析：作出点P关于OA的对称点E，作出点P关于OB的对称点F，连接EF，交OA于Q，交OB于R．连接PQ，PR，PE，PF，OE，OF，
则PQ=EQ，PR=RF，
则△PQR的周长=PQ+QR+PR=EQ+QR+R... 如图，△ACB和△DCE均为等腰三角形，点A、D、E在同一直线上，连接BF.若∠CAB＝∠CBA＝∠CDE＝∠CED＝50°.
(1)求证：AD＝BE；
(2)求∠AEB的度数．
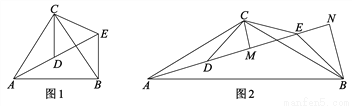
(1)见解析；（2）80°.
【解析】试题分析：（1）通过角的计算找出∠ACD=∠BCE，再结合△ACB和△DCE均为等腰三角形可得出“AC=BC，DC=EC”，利用全等三角形的判定（SAS）即可证出△ACD≌△BCE，由此即可得出结论AD=BE；
（2）结合（1）中的△ACD≌△BCE可得出∠ADC=∠BEC，再通过角的计算即可算出∠AEB的度数．
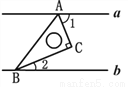
试题解析：（1）∵∠CAB＝... 
如图，直线AB∥ CD，∠ B=50°，∠ C=40°，则∠E等于（ ）
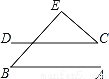
A. 70° B. 80° C. 90° D. 100°
C
【解析】试题分析：根据平行线的性质得到∠1=∠B=50°，由三角形的内角和定理可得∠E=180°﹣∠B﹣∠1=90°，故答案选C．