题目内容
如图,在△ABC中,AB=AD=DC,∠BAD=26°.求∠B和∠C的度数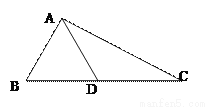
 77° 38.5°
【解析】【解析】
∵ AB=AD,
∴∠B=∠ADB. ……………… 2分
∵在△ABD中,∠B+∠ADB+∠BAD=180°,∠BAD=26°,
∴∠B=∠ADB=77°. ……………… 4分
∵AD.=DC,
∴∠DAC =∠C. ……………… 6分
∵∠ADB=∠DAC+∠C, ……………… 7分
∴∠ADB=2∠C,
...
77° 38.5°
【解析】【解析】
∵ AB=AD,
∴∠B=∠ADB. ……………… 2分
∵在△ABD中,∠B+∠ADB+∠BAD=180°,∠BAD=26°,
∴∠B=∠ADB=77°. ……………… 4分
∵AD.=DC,
∴∠DAC =∠C. ……………… 6分
∵∠ADB=∠DAC+∠C, ……………… 7分
∴∠ADB=2∠C,
...
练习册系列答案
相关题目
若2x=3,2y=5,求42x+y的值.
 2025
【解析】试题分析:逆用幂的运算法则解答即可.
试题解析:【解析】
因为2x=3,2y=5,所以42x+y=42x×4y=24x×22y=(2x)4×(2y)2=34×52=2 025.
2025
【解析】试题分析:逆用幂的运算法则解答即可.
试题解析:【解析】
因为2x=3,2y=5,所以42x+y=42x×4y=24x×22y=(2x)4×(2y)2=34×52=2 025. 用“>”或“<”填空:
(1)如果x-2<3,那么x______5; (2)如果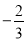 x<-1,那么x______
x<-1,那么x______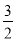 ;
;
(3)如果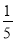 x>-2,那么x______-10;(4)如果-x>1,那么x______-1.
x>-2,那么x______-10;(4)如果-x>1,那么x______-1.
 < > > <
【解析】(1)如果x-2<3,那么x<5;
(2)如果,那么;
(3)如果,那么x>-10;
(4)如果-x>1,那么x<-1.
< > > <
【解析】(1)如果x-2<3,那么x<5;
(2)如果,那么;
(3)如果,那么x>-10;
(4)如果-x>1,那么x<-1. 如图,一艘轮船位于灯塔P的北偏东60°方向,与灯塔P的距离为30海里的A处,轮船沿正南方向航行一段时间后,到达位于灯塔P的南偏东30°方向上的B处,则此时轮船所在位置B与灯塔P之间的距离为( )
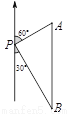
A. 60海里 B. 45海里 C. 20 海里 D. 30
海里 D. 30 海里
海里
 D
【解析】试题分析:根据条件易知△APB是直角三角形,AP=30,∠A=60°,∠B=30°,运用三角函数定义易求BP.
D
【解析】试题分析:根据条件易知△APB是直角三角形,AP=30,∠A=60°,∠B=30°,运用三角函数定义易求BP. 如图,△ACB和△DCE均为等腰三角形,点A、D、E在同一直线上,连接BF.若∠CAB=∠CBA=∠CDE=∠CED=50°.
(1)求证:AD=BE;
(2)求∠AEB的度数.
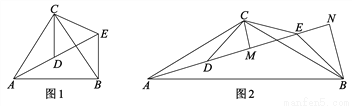
 (1)见解析;(2)80°.
【解析】试题分析:(1)通过角的计算找出∠ACD=∠BCE,再结合△ACB和△DCE均为等腰三角形可得出“AC=BC,DC=EC”,利用全等三角形的判定(SAS)即可证出△ACD≌△BCE,由此即可得出结论AD=BE;
(2)结合(1)中的△ACD≌△BCE可得出∠ADC=∠BEC,再通过角的计算即可算出∠AEB的度数.
试题解析:(1)∵∠CAB=...
(1)见解析;(2)80°.
【解析】试题分析:(1)通过角的计算找出∠ACD=∠BCE,再结合△ACB和△DCE均为等腰三角形可得出“AC=BC,DC=EC”,利用全等三角形的判定(SAS)即可证出△ACD≌△BCE,由此即可得出结论AD=BE;
(2)结合(1)中的△ACD≌△BCE可得出∠ADC=∠BEC,再通过角的计算即可算出∠AEB的度数.
试题解析:(1)∵∠CAB=... 等腰三角形一腰上的中线将它的周长分别为8和12两部分,则它的腰长、底边长分别为__________________.
 8,8,4或
【解析】设底边长a,腰长b,则有
(1)a+=8,
b+=12,
解得:a=4,b=8,
即腰长、底边长分别为:8,8,4;
(2)a+=12,
b+=8,
得a= ,b=,
即腰长、底边长分别为: , , ,
综上,腰长、底边长分别为:8,8,4或, , ,
故答案为:8,8,4或, , .
8,8,4或
【解析】设底边长a,腰长b,则有
(1)a+=8,
b+=12,
解得:a=4,b=8,
即腰长、底边长分别为:8,8,4;
(2)a+=12,
b+=8,
得a= ,b=,
即腰长、底边长分别为: , , ,
综上,腰长、底边长分别为:8,8,4或, , ,
故答案为:8,8,4或, , . 如图,在△ABC中,AD平分∠BAC,DE⊥AB于E,DF⊥AC于F,M为AD上任意一点,则下列结论中错误的是( )
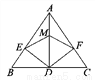
A. DE=DF B. ME=MF
C. AE=AF D. BD=CD
 D
【解析】∵AD平分∠BAC,DE⊥AB,DF⊥AC,
∴∠BAD=∠CAD,∠AED=∠AFD=90°,
又∵AD=AD,
∴△ADE≌△ADF,
∴DE=DF,AE=AF,
∵AE=AF,∠BAD=∠CAD,AM=AM,
∴△AME≌△AMF,
∴ME=MF,
故选项A、B、C正确,
无法得到BD=CD,故选项D错误,
故选D...
D
【解析】∵AD平分∠BAC,DE⊥AB,DF⊥AC,
∴∠BAD=∠CAD,∠AED=∠AFD=90°,
又∵AD=AD,
∴△ADE≌△ADF,
∴DE=DF,AE=AF,
∵AE=AF,∠BAD=∠CAD,AM=AM,
∴△AME≌△AMF,
∴ME=MF,
故选项A、B、C正确,
无法得到BD=CD,故选项D错误,
故选D... 如图,在△ABC中,∠C=90°,AB=13,BC=5,则sin A的值是( )

A. 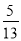 B.
B. 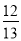 C.
C. 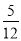 D.
D. 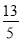
 A
【解析】【解析】
在Rt△ABC中,由勾股定理得,BC==12,∴sinA=,故选B.
A
【解析】【解析】
在Rt△ABC中,由勾股定理得,BC==12,∴sinA=,故选B. 分解因式:2a2b-5ab2
 ab(2a-5b)
【解析】试题分析:根据提公因式法分解因式,先确定公因式ab,再提取公因式即可.
试题解析:2a2b-5ab2= ab(2a-5b).
ab(2a-5b)
【解析】试题分析:根据提公因式法分解因式,先确定公因式ab,再提取公因式即可.
试题解析:2a2b-5ab2= ab(2a-5b). 
