题目内容
如图，AD是△ABC的角平分线，DE⊥AB于E，DF⊥AC于F，直线AD交EF于点O.问直线AD是线段EF的垂直平分线吗？请说明理由．
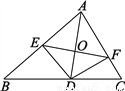
AD是线段EF的垂直平分线，理由见解析
【解析】试题分析：由AD为△ABC的角平分线，得到DE=DF，推出∠AEF和∠AFE相等，得到AE=AF，即可推出结论.
试题解析：∵AD为△ABC的角平分线，DE⊥AB，DF⊥AC，
∴DE=DF，∠AED=∠AFD=90°，
∴∠DEF=∠DFE，
∴∠AEF=∠AFE，
∴AE=AF，
∴点A、D都在EF的垂直...
练习册系列答案
阅读快车系列答案
相关题目
如图，点C，F，E，B在一条直线上，∠CFD＝∠BEA，CE＝BF，DF＝AE，写出CD与AB之间的关系，并证明你的结论．
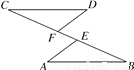
CD∥AB，CD＝AB，证明见解析.
【解析】试题分析:根据CE＝BF,可求证CF=BE,再根据∠CFD＝∠BEA,DF＝AE,
可证△DFC≌△AEB,利用全等三角形的性质可得: CD＝AB,∠C＝∠B,根据平行线的判定可证CD∥AB.
CD∥AB，CD＝AB，
证明如下：∵CE＝BF，∴CE－EF＝BF－EF，∴CF＝BE.
在△DFC和△AEB中，∴△DFC≌△... 若x＋y＞x－y，y－x＞y，那么
（1）x＋y＞0，（2）y－x＜0，（3）xy≤0，（4）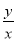
＜0中，
正确结论的序号为________.
（2）
【解析】
试题分析：由x＋y＞x－y，y－x＞y，可得x＜0，y＜0，再根据不等式的基本性质即可得到结果。
∵x＋y＞x－y，y－x＞y，
∴x＜0，y＜0，
∴x＋y＜0，y－x＜0，xy＞0，＞0，
则正确结论的序号为（2）. 下列命题中，其逆命题成立的是__．（只填写序号）
①同旁内角互补，两直线平行；
②如果两个角是直角，那么它们相等；
③如果两个实数相等，那么它们的平方相等；
④如果三角形的三边长a，b，c满足a2+b2=c2，那么这个三角形是直角三角形．
①④
【解析】把一个命题的条件和结论互换就得到它的逆命题，再分析逆命题是否为真命题，需要分别分析各题设是否能推出结论，从而利用排除法得出答案。
①两直线平行，同旁内角互补，正确；
②如果两个角相等，那么它们是直角，错误；
③如果两个实数的平方相等，那么这两个实数相等，错误；
④如果三角形的三边长a，b，c满足a2+b2=c2，那么这个三角形是直角三角形，正确．
... 如图，直线AB∥ CD，∠ B=50°，∠ C=40°，则∠E等于（ ）
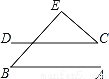
A. 70° B. 80° C. 90° D. 100°
C
【解析】试题分析：根据平行线的性质得到∠1=∠B=50°，由三角形的内角和定理可得∠E=180°﹣∠B﹣∠1=90°，故答案选C． 如图，已知△ABC是等边三角形，点B、C、D、E在同一直线上，且CG=CD，DF=DE，则∠E=______。
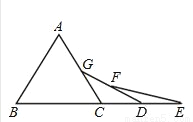
15°
【解析】试题分析：设∠E=x，根据等边对等角的性质以及三角形的一个外角等于与它不相邻的两个内角的和列式计算即可得解．
【解析】
设∠E=x，
∵DF=DE，
∴∠DFE=∠E=x，
∴∠CDG=∠E+∠DFE=2x，
∵CG=CD，
∴∠CDG=∠CGD=2x，
∴∠ACB=∠CDG+∠CGD=2x+2x=4x，
∵∠ACB=70°，... 如图，四边形ABCD中，∠BAD＝120°，∠B＝∠D＝90°，在BC、CD上分别找一个点M、N，使△AMN周长最小时，∠AMN＋∠ANM的度数为( )
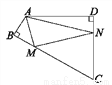
A. 130° B. 120°
C. 110° D. 100°
B
【解析】作A关于BC和CD的对称点A′，A″，连接A′A″，交BC于M，交CD于N，则A′A″即为△AMN的周长最小值，作DA延长线AH，
∵∠DAB=120°，
∴∠HAA′=60°，
∴∠AA′M+∠A″=∠HAA′=60°，
∵∠MA′A=∠MAA′，∠NAD=∠A″，
且∠MA′A+∠MAA′=∠AMN，∠NAD+∠A″=∠ANM，
∴∠AMN... 在△ABC中，若cosA=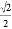
，tanB=
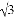，则这个三角形一定是（ ）
A. 锐角三角形 B. 直角三角形 C. 钝角三角形 D. 等腰三角形
A
【解析】试题解析：∵cosA=，tanB=，
∴∠A=45°，∠B=60°．
∴∠C=180°-45°-60°=75°．
∴△ABC为锐角三角形．
故选A． 计算：17×3.14＋61×3.14＋22×3.14；
314
【解析】试题分析：根据提公因式法分解因式，先确定公因式3.14，再提取公因式即可.
试题解析：17×3.14＋61×3.14＋22×3.14
=3.14×（17+61+22）
=3.14×100
=314