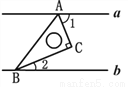
题目内容
如图，在等边三角形ABC中，∠B、∠C的平分线相交于点O，作BO、CO的垂直平分线分别交BC于点E、F.小明说：“E、F是BC的三等分点．”你同意他的说法吗？请说明理由．
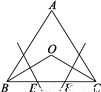
同意，理由见解析
【解析】试题分析：连接OE、OF，根据等边三角形角平分线的性质，可得∠OBC=∠OCB=30°，由BC的垂直平分线，可知BE=OE，∠EBO=∠EOB=30°，∠OEF=60°，再证，∠OFE=60°，得出△OEF为等边三角形，从而可知EF=OE=BE=OF=FC，得出结论．
试题解析：同意．理由如下：
连接OE、OF，
∵E为BO垂直平分线上的点，且∠O...
练习册系列答案
相关题目
在一次实验中，小明把一根弹簧的上端固定、在其下端悬挂物体，下面是测得的弹簧的长度y与所挂物体质量x的一组对应值．
所挂物体质量x/kg | 0 | 1 | 2 | 3 | 4 | 5 |
弹簧长度y/cm | 18 | 20 | 22 | 24 | 26 | 28 |
①上表反映了哪两个变量之间的关系？哪个是自变量？哪个是因变量？
②当所挂物体重量为3千克时，弹簧多长？不挂重物时呢？
③若所挂重物为7千克时（在允许范围内），你能说出此时的弹簧长度吗？
①上表反映了弹簧长度与所挂物体质量之间的关系；其中所挂物体质量是自变量，弹簧长度是因变量；②当所挂物体重量为3千克时，弹簧长24厘米；当不挂重物时，弹簧长18厘米；③32厘米．
【解析】试题分析：①因为表中的数据主要涉及到弹簧的长度和所挂物体的质量，所以反映了所挂物体的质量和弹簧的长度之间的关系，所挂物体的质量是自变量；弹簧的长度是因变量；
②由表可知，当物体的质量为3kg时，弹簧的长... x＜y得到ax＞ay的条件应是____________．
a＜0
【解析】∵x＜y得到ax＞ay是两边同时乘以a，不等号的方向发生了改变，∴a＜0． 如图，Rt△ABC中，AB=9，BC=6，∠B=90°，将△ABC折叠，使A点与BC的中点D重合，折痕为MN，则线段BN的长为（ ）
A. 
B. 
C. 4 D. 5
C
【解析】试题分析：设BN=x，由折叠的性质可得DN=AN=9－x，
∵D是BC的中点，
∴BD=3，
在Rt△BDN中，x2+32=（9－x）2，
解得x=4．
故线段BN的长为4．
故选C． 
已知等腰△ABC中，AB=AC，D是BC边上一点，连接AD，若△ACD和△ABD都是等腰三角形，则∠C的度数是 ．
36°或45°．
【解析】
试题分析：△ACD和△ABD都是等腰三角形，但没有说具体的边相等，所以应分情况讨论．
（1）AD=BD，DC=AD，那么△ADB和△ADC是全等三角形，可求得∠ADC=90°，那么∠C=45°；
（2）AB=BD，CD=AD，那么∠B=∠C=∠DAC，∠BAD=∠BDA=2∠C，然后用∠C表示出△ABC的内角和，即可求得5∠C=180°，那么∠C... 如图所示，四边形ABCD中，AE、AF分别是BC、CD的垂直平分线，∠EAF＝80°，∠CBD＝30°，则∠ADC的度数为( )
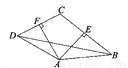
A. 45° B. 60°
C. 80° D. 100°
B
【解析】连接AC，
∵AE、AF分别是BC、CD的垂直平分线，
∴AB=AC=AD，
∵AF⊥DC，AE⊥BC，
∴∠CAF=∠DAF，∠CAE=∠BAE．
∴∠DAB=2∠EAF=160°，
∴∠ABD=（180°-160°）÷2=10°，
∴∠ABC=∠ACB=30°+10°=40°；
在四边形AECF中，
∠FCE=360°-9... 在△ABC中，已知AC=3，BC=4，AB=5，那么下列结论正确的是( )
A.sinA=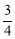
B.cosA=
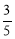C.tanA= 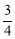D.cosB=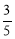
B
【解析】
试题分析：先根据勾股定理的逆定理判断△ABC的形状，再根据三角函数的定义依次分析各项即可.
∵
∴△ABC是直角三角形
∴，，，
故选B. 分解因式：2ab2－6a2b＋ab;
ab(2b－6a＋1)
【解析】试题分析：根据提公因式法分解因式，先确定公因式ab，再提取公因式即可.
试题解析：2ab2－6a2b＋ab = ab(2b－6a＋1).