如图所示，直线AB，CD相交于点O，OE平分∠AOC，若∠AOD-∠DOB=60°，则∠EOB=__________.
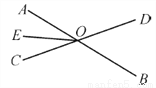
150°
【解析】∵∠AOD－∠BOD＝60°,
∴∠AOD=∠BOD+60°,
∵AB为直线,∴∠AOD+∠BOD=∠AOB=180°,
∴∠BOD+60°+∠BOD=180°,
∴∠BOD=60°,
∵∠AOC与∠BOD为对顶角,
∴∠AOC＝∠BOD=60°,
∵OE平分∠AOC,
∴∠AOE＝∠AOC=30°,
∴∠BOE=180... 如图所示，AB，CD，EF交于点O，∠1=20°，∠2=60°，求∠BOC的度数.
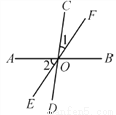
∠BOC=80°.
【解析】试题分析:根据∠2和∠BOF是对顶角,所以∠2=∠BOF,所以∠BOC=∠1+∠BOF=20°+60°=80°.
试题解析:因为∠BOF=∠2=60°,
所以∠BOC=∠1+∠BOF=20°+60°=80°. 如图所示，直线AB与CD相交于点O，OE平分∠AOD，∠BOC=80°，求∠BOD和∠AOE的度数.
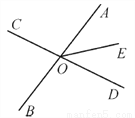
∠AOE=40°.
【解析】试题分析: 根据∠BOD与∠BOC是邻补角,∠BOC=80°,可求得:∠BOD=180°—∠BOC=100°,再根据∠AOD与∠BOC是对顶角,可得:∠AOD=∠BOC=80°,因为OE平分∠AOD,所以∠AOE=∠BOC=40°.
试题解析:因为∠BOD与∠BOC是邻补角,∠BOC=80°,
所以∠BOD=180°—∠BOC=100°,
又因为... 如图所示，l1，l2，l3交于点O，∠1＝∠2，∠3∶∠1＝8∶1，求∠4的度数．
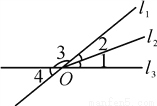
∠4＝36°
【解析】试题分析：设∠1=x，根据题意表示出∠2，再表示出∠3，然后根据邻补角的和等于180°列式求出x，再根据对顶角相等求出∠4即可．
【解析】
设∠1=x，则∠2=x，∠3=8x，依题意有
x+x+8x=180°，
解得x=18°，
则∠4=18°+18°=36°．
故∠4的度数是36°． 探究题：
（1）三条直线相交，最少有__________个交点，最多有__________个交点，分别画出图形，并数出图形中的对顶角和邻补角的对数；
（2）四条直线相交，最少有__________个交点，最多有__________个交点，分别画出图形，并数出图形中的对顶角和邻补角的对数；
（3）依次类推，n条直线相交，最少有__________个交点，最多有__________个交点，对顶角有__________对，邻补角有__________对.
(1)1，3；(2)1，6；(3)1， ，n(n-1)，2n(n-1)
【解析】（1）三条直线相交,最少有1个交点,最多有3个交点,如图：
（2）四条直线相交,最少有1个交点,最多有6个交点,如图:
（3）n条直线相交,最少有1个交点,最多有个交点,对顶角有对,邻补角有对.
故答案为:（1）1,3,（2）1,6,（3）1, , ,． 基本尺规作图包括:①作一条线段等于___________;②作一个角等于___________;③作一个角的___________;④作一条线段的___________;⑤过一点作已知直线的___________.
已知线段 已知角 平分线 垂直平分线 垂线
【解析】五个基本尺规作图：①作一条线段等于已知线段;②作一个角等于已知角;③作一个角的平分线;④作一条线段的垂直平分线;⑤过一点作已知直线的垂线.
故答案为：(1). 已知线段 (2). 已知角 (3). 平分线 (4). 垂直平分线 (5). 垂线. 尺规作图的画图工具是（ ）
A. 刻度尺、量角器 B. 三角板、量角器
C. 直尺、量角器 D. 没有刻度的直尺和圆规
D
【解析】试题分析：尺规作图的工具是指没有刻度的直尺、圆规．
故选：D
考点: 尺规作图的定义. 如图,用尺规作出∠OBF=∠AOB,作图痕迹
是( )
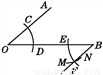
A. 以点B为圆心,OD为半径的弧 B. 以点B为圆心,DC为半径的弧
C. 以点E为圆心,OD为半径的弧 D. 以点E为圆心,DC为半径的弧
D
【解析】根据作一个角等于已知角的尺规作图的方法，易得D. 利用尺规作三角形,有三种基本类型:
(1)已知三角形的两边及其夹角,求作符合要求的三角形,其作图依据是“____”;
(2)已知三角形的两角及其夹边,求作符合要求的三角形,其作图依据是“____”;
(3)已知三角形的三边,求作符合要求的三角形,其作图依据是“____”.
SAS ASA SSS
【解析】根据SAS—两边及其夹角分别相等的两个三角形全等；ASA—两角及其夹边分别相等的两个三角形全等；SSS—三边分别相等的两个三角形全等.
故答案：(1)SAS、 (2)ASA 、(3)SSS. 已知三边作三角形,用到的基本作图是( )
A. 作一个角等于已知角 B. 作已知直线的垂线
C. 作一条线段等于已知线段 D. 作一条线段等于已知线段的和
C
【解析】已知三角形的三边,求作符合要求的三角形,其作图依据是“SSS”.故用到的基本作图是：作一条线段等于已知线段.
故选C.