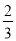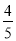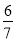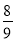题目内容
已知三边作三角形,用到的基本作图是( )
A. 作一个角等于已知角 B. 作已知直线的垂线
C. 作一条线段等于已知线段 D. 作一条线段等于已知线段的和
C
【解析】已知三角形的三边,求作符合要求的三角形,其作图依据是“SSS”.故用到的基本作图是：作一条线段等于已知线段.
故选C.
小华要设计一个摸球游戏,使得摸到红球的概率为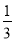
,如果设计符合要求,那么他周末就可以逛公园了,但妈妈对他的设计作出如下要求:(1)至少有四种颜色的球;
(2)至少有一个球是黄球.小华应该怎样设计呢?
答案见解析
【解析】试题分析：用6个球，其中2个红球，1个白球、1个蓝球，2个黄球，从而设计出摸球游戏．
试题解析：【解析】
用6个除颜色外完全相同的红球、白球、蓝球、黄球设计一个摸球游戏，其中2个红球，1个白球、1个蓝球，2个黄球． 一种饮料重约300g，罐上注有“蛋白质含量≥0.5%”，其中蛋白质的含量为多少克？
不少于1.5克
【解析】
试题分析：根据“蛋白质含量≥0.5%”，即可得到结果.
300×0.5%=1.5克
答：其中蛋白质的含量不少于1.5克. 用不等式表示图中的解集，其中正确的是( )
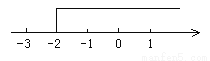
A. x≥－2 B. x＞－2 C. x＜－2 D. x≤－2
A
【解析】
试题分析：根据不等式的解集在数轴上表示出来的方法即可得到结果.
用不等式表示图中的解集为x≥－2，故选A. 如图,已知线段a,b和∠α=40°,你能作出符合如下要求的唯一三角形吗?AB=a,BC=b,∠A=∠α,若能,写出作法;若不能,请说明理由.
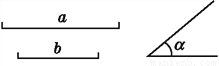
见解析
【解析】【试题分析】AB=a,BC=b,∠A=∠α，已知两边及其一边的对角，不能作出唯一的三角形.如下图.
【试题解析】
如图,能作出两个三角形:△ABC'和△ABC,所以不能作出唯一的符合要求的三角形.
理由:SSA不能说明两个三角形全等,所以一般情况下,已知两边和其中一边的对角不能作出唯一的三角形. 探究题：
（1）三条直线相交，最少有__________个交点，最多有__________个交点，分别画出图形，并数出图形中的对顶角和邻补角的对数；
（2）四条直线相交，最少有__________个交点，最多有__________个交点，分别画出图形，并数出图形中的对顶角和邻补角的对数；
（3）依次类推，n条直线相交，最少有__________个交点，最多有__________个交点，对顶角有__________对，邻补角有__________对.
(1)1，3；(2)1，6；(3)1， ，n(n-1)，2n(n-1)
【解析】（1）三条直线相交,最少有1个交点,最多有3个交点,如图：
（2）四条直线相交,最少有1个交点,最多有6个交点,如图:
（3）n条直线相交,最少有1个交点,最多有个交点,对顶角有对,邻补角有对.
故答案为:（1）1,3,（2）1,6,（3）1, , ,． 如图，点O在直线AB上，射线OC平分∠DOB．若∠COB=35°，则∠AOD等于( ).
A. 35° B. 70°
C. 110° D. 145°
C
【解析】∵OC平分∠DOB，∠COB=35°，
∴∠BOD=2∠COB=2×35°=70°,
∴∠AOD=180°-70°=110°.
故选D. 如图，△ABC沿直线l向右移了3厘米，得△FDE，且BC＝6厘米，∠B＝40°.
(1)求BE；
(2)求∠FDB的度数；
(3)找出图中相等的线段(不另添加线段)；
(4)找出图中互相平行的线段(不另添加线段)．
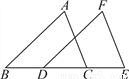
(1) 9厘米；(2) 140°；(3) AB＝FD、AC＝FE、BC＝DE、BD＝CE；(4) AB∥FD、AC∥FE.
【解析】试题分析：（1）根据平移的性质可得CE＝3cm，然后根据BE＝BC＋CE即可得出结论；
（2）根据平移的性质得出∠FDE的度数，然后根据邻补角互补即可得出答案；
（3）直接根据平移的性质即可得出结论；
（4）根据平移的性质即可得出结论．
... 宁宁同学设计了一个计算程序如下表:
输入数据 | 1 | 2 | 3 | 4 | 5 | … |
输出数据 |
|
|
|
|
| … |
根据表格中的数据的对应关系,可得出输出数据y与输入数据x之间的关系式为_____.
y=
【解析】【解析】
根据题意，得： ．故答案为： ．