求不等式
x+1＞0的解集和它的非负整数解，并把解集在数轴上表示出来．
非负整数解为0，1，2，3．数轴见解析
【解析】试题分析：首先解不等式求得不等式的解集，然后确定解集中的非负整数解即可．
试题解析：去分母得：-x+4＞0，
解得：x＜4．
则非负整数解为0，1，2，3． x取什么值时，代数式2x－5大于代数式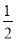
(2－x)的值？
x＞．
【解析】【试题分析】根据题意得不等式 ，得 得 得 x＞．
【试题解析】
由题意得： ，解得x＞．
故答案为x＞． |2a－24|＋（3a－b－k）2＝0，那么k取什么值时，b为负数．
k大于36时b为负数．
【解析】【试题分析】根据绝对值和完全平方的非负性，得 解得：a=12，b=36-k,当b<0时，即36-k<0，解得k>36.
【试题解析】
由题意得： 解得：b=36-k,
解得k>36.
故答案为k>36. 要使不等式－3x－a≤0的解集为x≥1，那么a应满足什么条件？
a=－3
【解析】【试题分析】解不等式－3x－a≤0，得 又因为不等式的解集为x≥1，则 解得a=-3.
【试题解析】 －3x－a≤0，
又它的解集为x≥1，
故答案是a=-3. 一堆有红、白两种颜色的球若干个，已知白球的个数比红球少，但白球的2倍比红球多．若把每一个白球都记作“2”，每一个红球都记作“3”，则总数为“60”，那么这两种球各有多少个？
白球有9个，红球有14个．
【解析】【试题分析】设白球有x个，红球有y个，根据“白球的个数比红球少，但白球的2倍比红球多”，得 ，解得7.5＜x＜12，则x可以取8,9,10,11.
由于2x=60－3y=3（20－y） 得2x应是3的倍数，则x只能取9，y = = 14
即白球有9个，红球有14个．
【试题解析】
设白球有x个，红球有y个，由题意，得
由第一个... 若一个三角形的两边长分别为3和7，则第三边长可能是( )
A. 6 B. 3
C. 2 D. 11
A
【解析】试题解析：设第三条边长为x，根据三角形三边关系得：
7-3＜x＜7+3，
即4＜x＜10.
结合各选项数值可知，第三边长可能是6.
故选A. 满足条件2∠A=2∠B=∠C的△ABC是( )
A. 锐角三角形 B. 等腰直角三角形
C. 钝角三角形 D. 不确定
B
【解析】试题解析：设∠A=x，则∠B=x，∠C=2x．又∠A+∠B+∠C=180°，
则则．
△ABC是等腰直角三角形．
故选B． 不一定在三角形内部的线段是( )
A. 三角形的角平分线 B. 三角形的中线
C. 三角形的高 D. 以上都不对
C
【解析】试题解析：三角形的角平分线、中线一定在三角形的内部，
直角三角形的高线有两条是三角形的直角边，
钝角三角形的高线有两条在三角形的外部，
所以，不一定在三角形内部的线段是三角形的高.
故选C. 已知△ABC≌△DEF，若AB=5，BC=6，AC=8，则△DEF的周长是( )
A. 8 B. 18
C. 19 D. 20
C
【解析】试题解析：∵AB=5，BC=6，AC=8，
∴△ABC的周长=AB+BC+AC=5+6+8=19，
∵△ABC≌△DEF，
∴△DEF的周长等于△ABC的周长，
∴△DEF的周长是19.
故选C. 如图，已知△ABC的六个元素，则下列甲、乙、丙三个三角形中和△ABC全等的图形是( )
A. 甲、乙 B. 甲、丙
C. 乙、丙 D. 甲、乙、丙
C
【解析】试题解析：由图形可知，甲有一边一角，不能判断两三角形全等，
乙有两边及其夹角，能判断两三角形全等，
丙得出两角及其一角对边，能判断两三角形全等，
根据全等三角形的判定得，乙丙正确.
故选C.