题目内容
满足条件2∠A=2∠B=∠C的△ABC是( )
A. 锐角三角形 B. 等腰直角三角形
C. 钝角三角形 D. 不确定
B
【解析】试题解析：设∠A=x，则∠B=x，∠C=2x．又∠A+∠B+∠C=180°，
则则．
△ABC是等腰直角三角形．
故选B．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
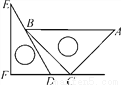
一副三角板如图放置，点C在FD的延长线上，AB∥CF，∠F＝∠ACB＝90°，∠E＝30°，∠A＝45°，AC＝12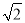
，试求CD的长．
CD＝12－4.
【解析】试题分析：过点B作BM⊥FD于点M，根据题意可求出BC的长度，然后在△EFD中可求出∠EDF=60°，求得MD的长，进而求得CD的长．
试题解析：
过点B作BM⊥FD于点M，
在△ACB中，∠ACB=90°，∠A=45°，AC=，
∴BC=AC=，∠ABC=45°，
∵AB∥CF，
∴∠BCM=∠ABC=45°，
∴BM＝B... 小杰想用6个除颜色外均相同的球设计一个游戏,下面是他设计的4个游戏方案.不成功的是( )
A. 摸到黄球的概率为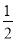
,红球的概率为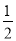
B. 摸到黄、红、白球的概率都为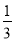
C. 摸到黄球的概率为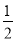
,红球的概率为
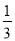,白球的概率为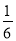
D. 摸到黄球的概率为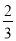
,摸到红球、白球的概率都是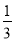
D
【解析】解：A．当6个球中有3个黄球，3个红球时，摸到黄球的概率为，红球为，故选项错误；
B．当6个球中有2个黄球，2个红球，2个白球时，摸到黄、红、白球的概率都为，故选项错误；
C．当6个球中有3个黄球，2个红球，1个白球时，摸到黄球的概率为，红球的概率为，白球为，故选项错误；
D． ++＞1，故摸到黄球的概率为，摸到红球、白球的概率都是是不成功的，故选项正确．
... 如图，在△ABC与△AEF中，AB=AE，BC=EF，∠B=∠E，AB交EF于点D.给出下列结论：①∠EAB=∠FAC；②AF=AC；③∠C=∠EFA；④AD=AC.其中正确的结论是_____(填序号)．
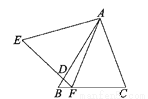
①②③
【解析】【解析】
在△AEF和△ABC中，∵AB=AE，∠B=∠E，BC=EF，∴△AEF≌△ABC（SAS），∴∠EAF=∠BAC，AF=AC，∠C=∠EFA，∴∠EAB=∠FAC，故①②③正确，④错误；
所以答案为：①②③． 如图，在△ABC中，CD是AB边上的高，BE是AC边的高，点O是两条高的交点，则∠A与∠1＋∠2的大小关系是( )
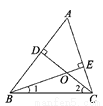
A. ∠A＞∠1＋∠2 B. ∠A=∠1＋∠2
C. ∠A＜∠1＋∠2 D. 无法确定
B
【解析】试题解析：∵CD是AB边上的高，BE是AC边上的高，
∴∠OEC=∠ADC=
又∴△ACD和△OCE中，∠ACD=∠OCE，
∴∠A=∠EOC
又∵∠EOC=∠1+∠2，
∴∠A=∠1+∠2.
故选B. x取什么值时，代数式2x－5大于代数式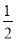
(2－x)的值？
x＞．
【解析】【试题分析】根据题意得不等式 ，得 得 得 x＞．
【试题解析】
由题意得： ，解得x＞．
故答案为x＞． 一个不等式的解集如图所示，则这个不等式的正整数解是________________.
x<3
【解析】试题解析：由图示可看出，从3出发向左画出的线，且3处是空心圆圈，表示x＜3．
所以这个不等式的解集为x＜3．
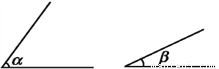
故正整数解为：1，2. 如图,已知∠α,∠β且∠α>∠β.求作∠γ,使∠γ=∠α-∠β.
见解析
【解析】【试题分析】运用基本作图“作一个角等于已知角”，作出∠α,∠β,根据两角之差即可.
【试题解析】
如图.
(1)作射线OA.
(2)以OA为一边,作∠BOA,使∠BOA=∠α.
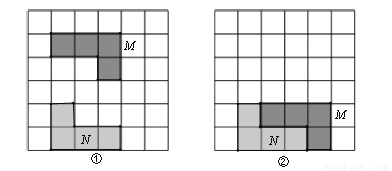
(3)以OB为一边在∠AOB内作∠BOC,使∠BOC=∠β,则∠AOC=∠α-∠β.故∠AOC=∠γ就是所求作的角. 如图，在6×6方格中有两个涂有阴影的图形M、N，①中的图形M平移后位置如图②所示，以下对图形M的平移方法叙述正确的是 （ ）
A. 向右平移2个单位，向下平移3个单位
B. 向右平移1个单位，向下平移3个单位
C. 向右平移1个单位，向下平移4个单位
D. 向右平移2个单位，向下平移4个单位
B
【解析】试题解析：根据图形M平移前后对应点的位置变化可知，图形M的平移方法为：向右平移1个单位，向下平移3个单位.
故选B.