题目内容
若一个三角形的两边长分别为3和7，则第三边长可能是( )
A. 6 B. 3
C. 2 D. 11
A
【解析】试题解析：设第三条边长为x，根据三角形三边关系得：
7-3＜x＜7+3，
即4＜x＜10.
结合各选项数值可知，第三边长可能是6.
故选A.
练习册系列答案
阅读快车系列答案
相关题目
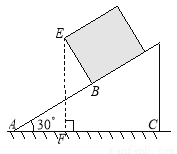
一个长方体木箱沿斜面下滑，当木箱滑至如图位置时，AB=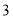
m，已知木箱高BE=
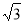m，斜坡角为30°，则木箱端点E距地面AC的高度EF为 m．
3.
【解析】
试题分析：连接AE，在Rt△ABE中求出AE，根据∠EAB的正切值求出∠EAB的度数，继而得到∠EAF的度数，在Rt△EAF中，解出EF即可得出答案．
试题解析：连接AE，
在Rt△ABE中，AB=3m，BE=m，
则AE=m，
又∵tan∠EAB=，
∴∠EAB=30°，
在Rt△AEF中，∠EAF=∠EAB+∠BAC=60°，
... 用8个除颜色外均相同的球设计一个游戏,使摸到白球与摸不到白球的可能性一样大,摸到红球的可能性比摸到黄球的可能性大,则游戏设计中白、红、黄球的个数可能是( )
A. 4,2,2 B. 3,2,3 C. 4,3,1 D. 5,2,1
C
【解析】【解析】
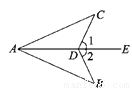
∵摸到白球与摸不到白球的可能性一样大，摸到红球的可能性比摸到黄球的可能性大，∴白球4个，红球3个，黄球1个．故选C． 如图，∠1=∠2，要使△ABD≌△ACD，需添加的一个条件是_________
∠B=∠C等
【解析】试题解析：需添加的一个条件是：∠B=∠C，
理由：∵∠1=∠2，
∴∠ADC=∠ADB，
在△ABD和△ACD中，
∴△ABD≌△ACD(AAS).
故答案为：∠B=∠C.(答案不唯一). 如图，Rt△ABC中，AB⊥AC，AD⊥BC，BE平分∠ABC交AD于点E，EF∥AC，下列结论一定成立的是( )
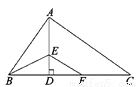
A. AB=BF B. AE=ED
C. AD=DC D. ∠ABE=∠DFE
A
【解析】【解析】
∵∠BAD+∠ABD=90°，∠ABD+∠C=90°
∴∠BAD=∠C（同角的余角相等）
又∵EF∥AC
∴∠BFE=∠C
∴∠BAD=∠BFE
又∵BE平分∠ABC
∴∠ABE=∠FBE
∴∠BEF=∠AEB，
在△ABE与△FBE中，
∠BEF=∠AEB，BE=BE，∠ABE=∠FBE
∴△ABE≌△FB... 求不等式
x+1＞0的解集和它的非负整数解，并把解集在数轴上表示出来．
非负整数解为0，1，2，3．数轴见解析
【解析】试题分析：首先解不等式求得不等式的解集，然后确定解集中的非负整数解即可．
试题解析：去分母得：-x+4＞0，
解得：x＜4．
则非负整数解为0，1，2，3． 直接想出不等式的解集：
（1）x＋3＞6的解集 ；（2）2x＜12的解集 ；
（3）x－5＞0的解集 ；（4）0.5x＞5的解集 .
（1）x＞3；（2）x＜6；（3）x＞5；（4）x＞10
【解析】
试题分析：根据不等式的基本性质即可得到结果.
（1）x＋3＞6的解集为x＞3；（2）2x＜12的解集为x＜6；
（3）x－5＞0的解集为x＞5；（4）0.5x＞5的解集为x＞10. 如图,已知线段a,c,∠α.
求作△ABC,使BC=a,AB=c,∠ABC=∠α.
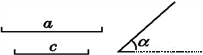
见解析
【解析】【试题分析】利用“SAS”原理作图.
【试题解析】
(1)作∠MBN=∠α.
(2)在射线BM上截取BA=c,在射线BN上截取BC=a.
(3)连接AC,则△ABC即为所求作的三角形(如图). 下列平移作图错误的是（ ）.
A.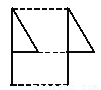 
B. 
C. 
D. 
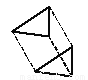C
【解析】试题分析：A、B、D符合平移变换，C是轴对称变换．
故选C．