题目内容
求不等式
x+1＞0的解集和它的非负整数解，并把解集在数轴上表示出来．
非负整数解为0，1，2，3．数轴见解析
【解析】试题分析：首先解不等式求得不等式的解集，然后确定解集中的非负整数解即可．
试题解析：去分母得：-x+4＞0，
解得：x＜4．
则非负整数解为0，1，2，3．
口算题卡加应用题集训系列答案
综合自测系列答案等腰三角形底边与底边上的高的比是2：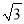 
，则顶角为（ ）
A. 60° B. 90° C. 120° D. 150°
A
【解析】如图，在△ABC中，AB=AC，AD⊥CB于D，
依题意得CD：AD=1： =:3，而tan∠DAC=CD：AD，
∴tan∠DAC=:3
∴∠DAC=30°，
∴顶角∠BAC=60°．
故选A． 在△ABC中，∠ACB=90°，AC=BC，直线MN经过点C，且AD⊥MN于D，BE⊥MN于E.
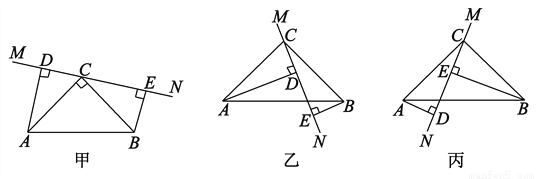
(1)当直线MN绕点C旋转到图甲的位置时，试说明：①△ADC≌△CEB；②DE=AD＋BE；
(2)当直线MN绕点C旋转到图乙的位置时，试说明：DE=AD－BE；
(3)当直线MN绕点C旋转到图丙的位置时，试问DE、AD、BE具有怎样的等量关系？请写出这个等量关系，并加以证明．
（1）证明见解析；（）证明见解析；（3）AD、DE、BE所满足的等量关系是DE=BE－AD(或AD=BE－DE，BE=AD＋DE等)理由见解析.
【解析】试题分析：（1）由∠ACB=90°，得∠BCE＋∠ACD=90°，而AD⊥MN于D，BE⊥MN于E.则∠ADC=∠CEB=90°，根据等角的余角相等得到∠ACD=∠CBE.，易得
Rt△ADC≌Rt△CEB，所以AD=CE，DC=BE... 根据下列已知条件，能画出唯一△ABC的是( )
A. AB=3，BC=4，CA=8 B. AB=4，BC=3，∠A=30°
C. ∠A=60°，∠B=45°，AB=4 D. ∠C=90°，AB=6
C
【解析】由一定的已知条件画三角形，要使画出的三角形是唯一的，说明不同的人根据这些条件画出的三角形一定是全等的；而由全等三角形的判定方法可知当两个三角形满足A、B、D选项中的边、角对应相等时，两个三角形不一定全等，只有满足C中的边、角对应相等时，可以由“ASA”判定两三角形全等.故选C. 若一个三角形的两边长分别为3和7，则第三边长可能是( )
A. 6 B. 3
C. 2 D. 11
A
【解析】试题解析：设第三条边长为x，根据三角形三边关系得：
7-3＜x＜7+3，
即4＜x＜10.
结合各选项数值可知，第三边长可能是6.
故选A. 恩格尔系数n是指家庭日常饮食开支占家庭收入的比例，它反映了居民家庭的实际生活水平，各种类型家庭的n值如下所示：
家庭类型 | 贫困 | 温饱 | 小康 | 发达国家 | 最富裕国家 |
n | 75%以上 | 50%～75% | 40%～49% | 20%～39% | 不到20% |
如用含n的不等式表示，则贫困家庭为 ；小康家庭为 ；最富裕国家为 ；当某一家庭n＝0.6时，表明该家庭的实际生活水平是 .
n＞75%，40%≤n≤49%，n＜20％，温饱
【解析】
试题分析：仔细分析表中数据即可得到结果.
如用含n的不等式表示，则贫困家庭为n＞75%；小康家庭为40%≤n≤49%；最富裕国家为n＜20％；当某一家庭n＝0.6时，表明该家庭的实际生活水平是温饱. 不等式的解集在数轴上表示如图所示，则该不等式可能是___________________.
不唯一，如x－1≤0
【解析】由图形可知，不等式的解集为x≤1.只要所写的不等式的解集为x≤1，即可，答案不唯一. 根据下列已知条件,能唯一画出△ABC的是( )
A. ∠A=36°,∠B=45°,AB=4 B. AB=4,BC=3,∠A=30°
C. AB=3,BC=4,CA=1 D. ∠C=90°,AB=6
A
【解析】A. ∠A=36°,∠B=45°,AB=4,利用原理“ASA”可以画出唯一的三角形；B、C、D都不能唯一的作出三角形.故选A. 用计算器求下列格式的值（结果精确到0.0001）．
（1）tan63°27′；
（2）cos18°59′27″；
（3）sin67°38′24″．
（1）2.0013；（2）0.9456；（3）0.9248．
【解析】试题分析：将度、分、秒统一为度，然后利用计算器即可求出结果．
试题解析：
【解析】
（1）tan63°27′=tan63.45°≈2.0013；
（2）cos18°59′27″=cos18.9908°≈0.9456；
（3）sin67°38′24″=sin67.64°≈0.9248．