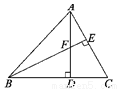
如图，在△ABC中，AD⊥BC于D，BE⊥AC于E，AD=BD=5，则AF＋CD=___.
5
【解析】试题解析：∵AD⊥BC于D，BE⊥AC于E，
≌
故答案为：5. 如图，A、B、C分别是线段A1B、B1C、C1A的中点，若△ABC的面积是1，那么△A1B1C1的面积为____.
7
【解析】试题分析：如下图，连接A1C，B1A，C1B，，因B是线段B1C的中点，所以B1B="BC." △A1B1A和△AB1B等底同高，根据等底同高的两个三角形面积相等可得S△B1AB=S△ABC=1；同理可得S△A1B1A=S△AB1B=1；所以=S△A1B1A+S△AB1B=1+1=2；同理可得S△C1CB1=2， S△C1AA1=2.
S△A1B1C1= S△A1BB1+ ... 在△ABC中，AB=AC=12cm，BC=6cm，D为BC的中点，动点P从B点出发，以每秒1cm的速度沿B→A→C的方向运动，设运动时间为t，那么当t=_________秒时，过D、P两点的直线将△ABC的周长分成两个部分，使其中一部分是另一部分的2倍．
7或17
【解析】试题解析：分两种情况：
（1）P点在AB上时，如图，
∵AB=AC=12cm，BD=CD=BC=×6=3cm，
设P点运动了t秒，则BP=t，AP=12-t，由题意得：
BP+BD=（AP+AC+CD）或（BP+BD）=AP+AC+CD，
∴t+3=（12-t+12+3）①或（t+3）=12-t+12+3②，
解①得t=7秒，解②得，t=... 如图，在△ABC中，∠BAC是钝角，画出：
(1)∠BAC的平分线；
(2)AC边上的中线；
(3)AC边上的高；
(4)AB边上的高．
作图见解析.
【解析】试题分析：（1）根据作已知角的角平分线的步骤作出图形；
（2）关键是找出线段AC的中点，要作出线段AC的垂直平分线，将所得中点与点B连结即可得到AC边上的中线；
（3）（4）根据过一点作已知直线垂线的方法，作出AC和AB边上的高，
试题解析：（1）∠BAC的平分线作法如下：
①以点A为圆心，定长为半径画弧，分别交AB、AC于D、E两点；
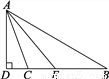
②... 如图，AD⊥BD，AE平分∠BAC，∠B=30°，∠ACD=70°.求∠DAE的度数．
40°.
【解析】试题分析：根据三角形的内角和求出根据∠ACD=70°，求出的度数，求出根据角平分线的性质求出
即可求解.
试题解析：
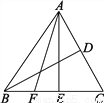
∵AE平分∠BAC， 如图，△ABC中，AE⊥BC，BD是AC边的中线，BF=1，BF∶FC=1∶3，△ABD的面积为2，求AE的长．
AE=2
【解析】试题分析：根据中线能够把三角形的面积分成相等的两部分，求出的面积，根据三角形的面积公式求出AE的长.
试题解析：BD是AC边的中线， 如图，在△ABC和△CED中，AB∥CD，AB=CE，AC=CD.求证：∠B=∠E.
证明见解析.
【解析】试题分析：根据AB//CD得出∠DCA=∠CAB，结合AB=CE，AC=CD得出△CAB≌△DCE，从而得出答案.
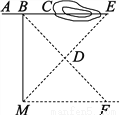
试题解析：∵AB//CD，∴∠DCA=∠CAB 又∵AB=CE，AC=CD，∴△CAB≌△DCE ∴∠B=∠E. 如图，沿AC方向开山修路，为了加快施工进度，要在山的另一边同时施工，工人师傅在AC上取一点B，在小山外取一点D，连接BD，并延长使DF=BD，过F点作AB的平行线段MF，连接MD，并延长，在其延长线上取一点E，使DE=DM，在E点开工就能使A、C、E成一条直线，你知道其中的道理吗？
说明见解析
【解析】试题分析：首先证明≌，可得进而得到BE∥MF，再由∥MF根据过直线外一点有且只有一条直线与已知直线平行，可得A、C、E三点在一条直线上．
试题解析：
≌
∴BE∥MF，
∵AB∥MF，
根据过直线外一点有且只有一条直线与已知直线平行，
在一条直线上． 如图所示，已知B、E分别是线段AC、DF的中点，AC=DF，BF交CD于点H，AE交CD于点G，CH=HG=DG，BH=GE.
(1)填空：因为B、E分别是线段AC、DF的中点，所以CB=________AC，DE=________DF.因为AC=DF，所以CB=________.在△CBH和△DEG中，因为CB=________，CH=________，BH=________EG，所以________≌________(SSS)．
(2)除了(1)中的全等三角形外，请你再写出另外一对全等三角形，并说明理由．
(1) ， ，DE，DE，DG，△CBH，△DEG. （2）证明见解析.
【解析】试题分析：（1）因为B是AC的中点， 同理因为AC=DF，由上知根据上面求得： 即可得△CBH≌△DEG.两个三角形对应的三边相等，则两个三角形全等，所以找出三角形对应的三边
（2）根据题中条件分析，再用SAS来证明即可
试题解析：（1）因为B是AC的中点， 同理
因为AC=DF，由上知根据上... 在△ABC中，∠ACB=90°，AC=BC，直线MN经过点C，且AD⊥MN于D，BE⊥MN于E.
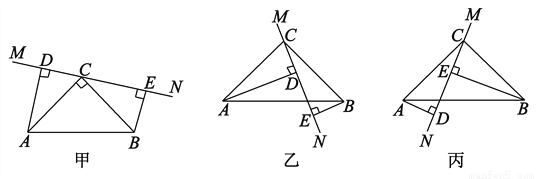
(1)当直线MN绕点C旋转到图甲的位置时，试说明：①△ADC≌△CEB；②DE=AD＋BE；
(2)当直线MN绕点C旋转到图乙的位置时，试说明：DE=AD－BE；
(3)当直线MN绕点C旋转到图丙的位置时，试问DE、AD、BE具有怎样的等量关系？请写出这个等量关系，并加以证明．
（1）证明见解析；（）证明见解析；（3）AD、DE、BE所满足的等量关系是DE=BE－AD(或AD=BE－DE，BE=AD＋DE等)理由见解析.
【解析】试题分析：（1）由∠ACB=90°，得∠BCE＋∠ACD=90°，而AD⊥MN于D，BE⊥MN于E.则∠ADC=∠CEB=90°，根据等角的余角相等得到∠ACD=∠CBE.，易得
Rt△ADC≌Rt△CEB，所以AD=CE，DC=BE...