题目内容
如图所示，已知B、E分别是线段AC、DF的中点，AC=DF，BF交CD于点H，AE交CD于点G，CH=HG=DG，BH=GE.
(1)填空：因为B、E分别是线段AC、DF的中点，所以CB=________AC，DE=________DF.因为AC=DF，所以CB=________.在△CBH和△DEG中，因为CB=________，CH=________，BH=________EG，所以________≌________(SSS)．
(2)除了(1)中的全等三角形外，请你再写出另外一对全等三角形，并说明理由．
(1) ， ，DE，DE，DG，△CBH，△DEG. （2）证明见解析.
【解析】试题分析：（1）因为B是AC的中点， 同理因为AC=DF，由上知根据上面求得： 即可得△CBH≌△DEG.两个三角形对应的三边相等，则两个三角形全等，所以找出三角形对应的三边
（2）根据题中条件分析，再用SAS来证明即可
试题解析：（1）因为B是AC的中点， 同理
因为AC=DF，由上知根据上...
在△ABC中，∠C-90°，若tanB=2，a=1，则b=________．
2
【解析】试题解析：在Rt△ABC中，
∵∠C=90°，
∴AB为斜边．
∴b=AC•tanB
=a•tanB
=2．
故答案为：2. 下列说法中，正确的是（ ）
A. 不可能事件发生的概率为0
B. 随机事件发生的概率为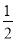
C. 概率很小的事件不可能发生
D. 投掷一枚质地均匀的硬币100次，正面朝上的次数一定为50次
A
【解析】试题分析：不可能事件发生的概率为0，故A正确；
随机事件发生的概率为在0到1之间，故B错误；
概率很小的事件也可能发生，故C错误；
投掷一枚质地均匀的硬币100次，正面向上的次数为50次是随机事件，D错误；
故选A． 小球在如图所示的地板上自由滚动，并随机地停留在某块方砖上，每一块方砖除颜色外完全相同，它最终停留在黑色方砖上的概率是 ．
.
【解析】
试题分析：根据几何概率的求法：最终停留在黑色的方砖上的概率就是黑色区域的面积与总面积的比值．观察这个图可知：黑色区域（4块）的面积占总面积（9块）的，则它最终停留在黑色方砖上的概率是.
故答案为：． 某口袋中有20个球,每个球除颜色外都相同,其中白球x个,绿球2x个,其余为黑球,甲从袋中任意摸出一个球,若为绿球则获胜,甲摸出的球放回袋中,乙从袋中摸出一个球,若为黑球则获胜.若对甲、乙双方公平,则x等于( )
A. 3 B. 4 C. 5 D. 6
B
【解析】【解析】
根据题意得： ，即2x=20-x-2x，解得：x=4．故选B． 如图，在△ABC中，∠BAC是钝角，画出：
(1)∠BAC的平分线；
(2)AC边上的中线；
(3)AC边上的高；
(4)AB边上的高．
作图见解析.
【解析】试题分析：（1）根据作已知角的角平分线的步骤作出图形；
（2）关键是找出线段AC的中点，要作出线段AC的垂直平分线，将所得中点与点B连结即可得到AC边上的中线；
（3）（4）根据过一点作已知直线垂线的方法，作出AC和AB边上的高，
试题解析：（1）∠BAC的平分线作法如下：
①以点A为圆心，定长为半径画弧，分别交AB、AC于D、E两点；
②... 如图，在△ABC中，点P是△ABC三条角平分线的交点，则∠PBC＋∠PCA＋∠PAB=___度．
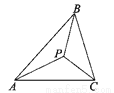
90
【解析】试题分析：由在△ABC中，点P是△ABC的内心，根据三角形的内心是三角形三条角平分线的交点，即可得∠PBC=∠ABC，∠PCA=∠ACB，∠PAB=∠BAC，又由三角形内角和定理，即可求得∠PBC+∠PCA+∠PAB的度数．
试题解析：∵在△ABC中，点P是△ABC的内心，
∴∠PBC=∠ABC，∠PCA=∠ACB，∠PAB=∠BAC，
∵∠ABC+∠BCA+... 求不等式1＋x＞x－1成立的x取值范围.
x可取一切实数
【解析】
试题分析：根据不等式的基本性质求出不等式1＋x＞x－1的解集即可判断.
不等式1＋x＞x－1两边同时减去x得1＞－1，恒成立
则不等式1＋x＞x－1成立的x取值范围是x可取一切实数. 如图，若∠1+∠3=180°，则图中与∠1相等的角有__________个，与∠1互补的角有__________个.
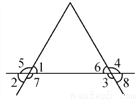
3 4
【解析】因为∠1和∠5,∠1和∠7,∠3和∠6,∠3和∠8是邻补角,所以∠1+∠5=180°, ∠1+∠7=180°, ∠3+∠6=180°, ∠3+∠8=180°,因为∠1+∠3=180°,所以∠1=∠6, ∠1=∠8,
因为∠1和∠2,所以∠1=∠2,故答案为:3,4.