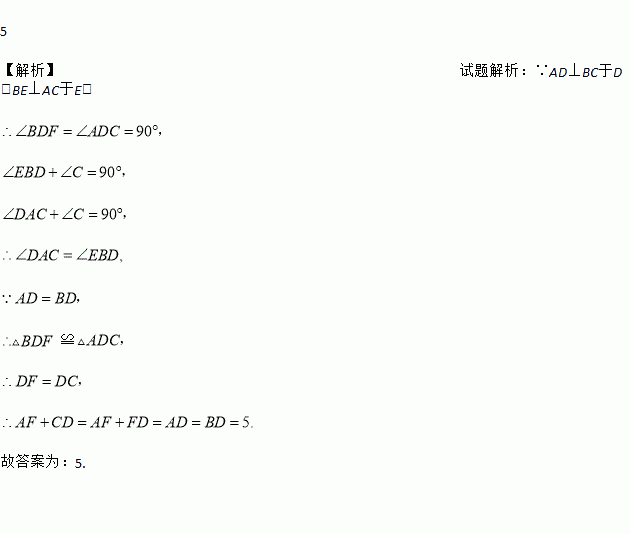题目内容
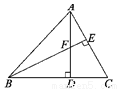
如图，在△ABC中，AD⊥BC于D，BE⊥AC于E，AD=BD=5，则AF＋CD=___.
5
【解析】试题解析：∵AD⊥BC于D，BE⊥AC于E，
≌
故答案为：5.
练习册系列答案
相关题目
在△ABC中，AB＝AC，且BC＝8cm，BD是腰AC的中线，△ABC的周长分为两部分，已知它们的差为2cm，则等腰三角形的腰长为__________.
10cm或6cm
【解析】如图∵BD是腰AC的中线，
∴AD=CD，
①当△ABD的周长与△BCD的周长差为2时，即AB+AD+BD-(BD+BC+CD)=2,
∴AB-BC=2,
∵BC=8cm，
∴AB=10cm.
②当△BCD的周长与△ABD的周长差为2时，即BD+BC+CD -(AB+AD+BD)=2,
∴BC - AB =2,
∵BC... 小明家里的阳台地面,水平铺设着仅黑白颜色不同的18块方砖(如图),他从房间里向阳台抛小皮球,小皮球最终随机停留在某块方砖上.
(1)求小皮球分别停留在黑色方砖与白色方砖上的概率.
(2)(1)中哪个概率较大?要使这两个概率相等,应改变哪块方砖的颜色?
（1）， (2)小皮球停留在黑色方砖上的概率大.
【解析】试题分析：（1）根据小球停在黑色方砖上的概率就是黑色方砖面积与总面积的比值，小球停在白色方砖上的概率就是白色方砖面积与总面积的比值，再根据黑色方砖、白色方砖的个数与总个数之间的关系，即可求出答案；
（2）要想这两个概率相等，只要使黑色方砖的个数与白色方砖的个数相等即可．
试题解析：【解析】
（1）∵白色方砖8块，黑色方砖... 一个箱子中放有红、黑、黄三种小球,每个球除颜色外都相同,三个人先后去摸球,一人摸一次,一次摸出一个小球,摸出后放回,摸出黑色小球为赢.这个游戏是( )
A. 公平的 B. 先摸者赢的可能性大 C. 不公平的 D. 后摸者赢的可能性大
A
【解析】【解析】
∵一个箱子中放有红、黄、黑三种小球，三个人先后去摸球，一人摸一次，一次摸出一个小球，摸出后放回，∴三个人摸到每种球的概率均相等，故这个游戏是公平的．故选A． 如图，△ABC中，AE⊥BC，BD是AC边的中线，BF=1，BF∶FC=1∶3，△ABD的面积为2，求AE的长．
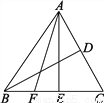
AE=2
【解析】试题分析：根据中线能够把三角形的面积分成相等的两部分，求出的面积，根据三角形的面积公式求出AE的长.
试题解析：BD是AC边的中线， 已知四条线段的长分别为2、3、4、5，用其中的三条线段构成的三角形的周长是_____________.
9或11或12
【解析】试题解析：由四条线段组成三角形的情况有：2，3，4；2，4，5；3，4，5，
故周长为9或11或12.
故答案为：9或11或12. 已知△ABC≌△DEF，若AB=5，BC=6，AC=8，则△DEF的周长是( )
A. 8 B. 18
C. 19 D. 20
C
【解析】试题解析：∵AB=5，BC=6，AC=8，
∴△ABC的周长=AB+BC+AC=5+6+8=19，
∵△ABC≌△DEF，
∴△DEF的周长等于△ABC的周长，
∴△DEF的周长是19.
故选C. 不等式x+3≤6的正整数解为___________________．
x＝1，2，3
【解析】x+3≤6，解得x≤3,故原不等式的正整数解为x＝1，2，3.故答案为x＝1，2，3. 下列说法中，正确的是( )
A. 相等的两个角是对顶角
B. 有一条公共边的两个角是邻补角
C. 有公共顶点的两个角是对顶角
D. 一条直线与端点在这条直线上的一条射线组成的两个角是邻补角
D
【解析】A选项,因为对顶角是一个角的两边分别是另一个角的反向延伸线,这两个角是对顶角两条直线相交后所得的只有一个公共顶点且两个角的两边互为反向延长线,这样的两个角叫做互为对顶角.两条直线相交,构成两对对顶角.互为对顶角的两个角相等.但相等的两个角不一定是对顶角,所以A选项错误,
B选项, 因为邻补角是有一条公共边,且一个角的一边是另一个角一边的反向延长线组成的2个角, 有一条公共边...