题目内容
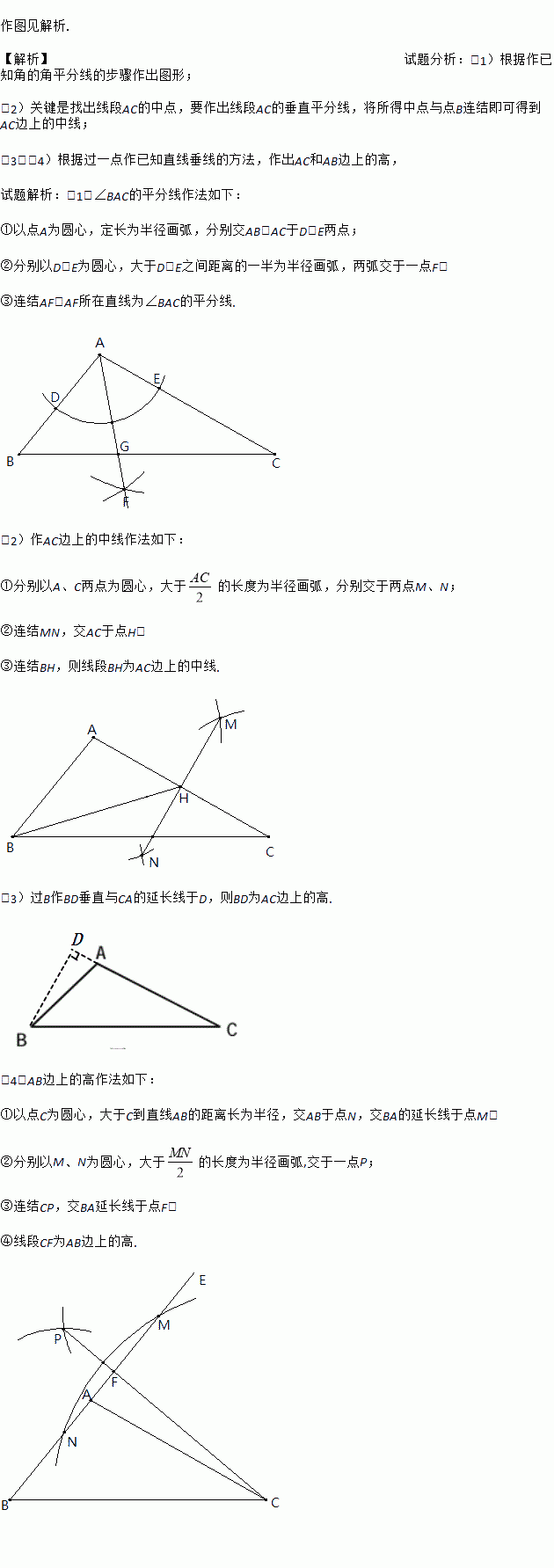
如图，在△ABC中，∠BAC是钝角，画出：
(1)∠BAC的平分线；
(2)AC边上的中线；
(3)AC边上的高；
(4)AB边上的高．
作图见解析.
【解析】试题分析：（1）根据作已知角的角平分线的步骤作出图形；
（2）关键是找出线段AC的中点，要作出线段AC的垂直平分线，将所得中点与点B连结即可得到AC边上的中线；
（3）（4）根据过一点作已知直线垂线的方法，作出AC和AB边上的高，
试题解析：（1）∠BAC的平分线作法如下：
①以点A为圆心，定长为半径画弧，分别交AB、AC于D、E两点；
②...
小学教材全测系列答案一个直角三角形有两条边长为3，4，则较小的锐角约为（ ）
A. 37° B. 41° C. 37°或41° D. 以上答案均不对
C
【解析】试题解析：①若3、4是直角边，
∵两直角边为3，4，
∴斜边长==5，
∴较小的锐角所对的直角边为3，则其正弦值为；
②若斜边长为4，则较小边=≈2.65，
∴较小边所对锐角正弦值约==0.6625，
利用计算器求得角约为37°或41°．
故选C． 设一个试验的所有可能的结果有n种,每次试验有且只有其中的一种结果出现.如果每种结果出现的_____________相同,那么我们就称这个试验的结果是_____________.
可能性; 等可能的
【解析】【解析】
如果每种结果出现的可能性相同，那么我们就称这个试验的结果是等可能的．故答案为：可能性，等可能的． 小杰想用6个除颜色外均相同的球设计一个游戏,下面是他设计的4个游戏方案.不成功的是( )
A. 摸到黄球的概率为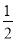
,红球的概率为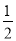
B. 摸到黄、红、白球的概率都为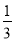
C. 摸到黄球的概率为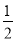
,红球的概率为
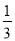,白球的概率为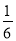
D. 摸到黄球的概率为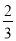
,摸到红球、白球的概率都是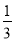
D
【解析】解：A．当6个球中有3个黄球，3个红球时，摸到黄球的概率为，红球为，故选项错误；
B．当6个球中有2个黄球，2个红球，2个白球时，摸到黄、红、白球的概率都为，故选项错误；
C．当6个球中有3个黄球，2个红球，1个白球时，摸到黄球的概率为，红球的概率为，白球为，故选项错误；
D． ++＞1，故摸到黄球的概率为，摸到红球、白球的概率都是是不成功的，故选项正确．
... 如图所示，已知B、E分别是线段AC、DF的中点，AC=DF，BF交CD于点H，AE交CD于点G，CH=HG=DG，BH=GE.
(1)填空：因为B、E分别是线段AC、DF的中点，所以CB=________AC，DE=________DF.因为AC=DF，所以CB=________.在△CBH和△DEG中，因为CB=________，CH=________，BH=________EG，所以________≌________(SSS)．
(2)除了(1)中的全等三角形外，请你再写出另外一对全等三角形，并说明理由．
(1) ， ，DE，DE，DG，△CBH，△DEG. （2）证明见解析.
【解析】试题分析：（1）因为B是AC的中点， 同理因为AC=DF，由上知根据上面求得： 即可得△CBH≌△DEG.两个三角形对应的三边相等，则两个三角形全等，所以找出三角形对应的三边
（2）根据题中条件分析，再用SAS来证明即可
试题解析：（1）因为B是AC的中点， 同理
因为AC=DF，由上知根据上... 如图，在△ABC与△AEF中，AB=AE，BC=EF，∠B=∠E，AB交EF于点D.给出下列结论：①∠EAB=∠FAC；②AF=AC；③∠C=∠EFA；④AD=AC.其中正确的结论是_____(填序号)．
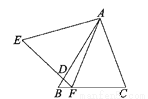
①②③
【解析】【解析】
在△AEF和△ABC中，∵AB=AE，∠B=∠E，BC=EF，∴△AEF≌△ABC（SAS），∴∠EAF=∠BAC，AF=AC，∠C=∠EFA，∴∠EAB=∠FAC，故①②③正确，④错误；
所以答案为：①②③． 如图，在△ABC中，CD是AB边上的高，BE是AC边的高，点O是两条高的交点，则∠A与∠1＋∠2的大小关系是( )
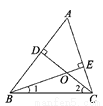
A. ∠A＞∠1＋∠2 B. ∠A=∠1＋∠2
C. ∠A＜∠1＋∠2 D. 无法确定
B
【解析】试题解析：∵CD是AB边上的高，BE是AC边上的高，
∴∠OEC=∠ADC=
又∴△ACD和△OCE中，∠ACD=∠OCE，
∴∠A=∠EOC
又∵∠EOC=∠1+∠2，
∴∠A=∠1+∠2.
故选B. 一个不等式的解集如图所示，则这个不等式的正整数解是________________.
x<3
【解析】试题解析：由图示可看出，从3出发向左画出的线，且3处是空心圆圈，表示x＜3．
所以这个不等式的解集为x＜3．
故正整数解为：1，2. 如图是一把剪刀，其中∠1=40°，则∠2= 度，其理由是 。
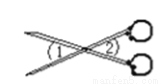
40°、对顶角相等.
【解析】
试题分析：根据图示可得∠1和∠2为对顶角，根据对顶角的性质求出角的度数.