题目内容
如图，沿AC方向开山修路，为了加快施工进度，要在山的另一边同时施工，工人师傅在AC上取一点B，在小山外取一点D，连接BD，并延长使DF=BD，过F点作AB的平行线段MF，连接MD，并延长，在其延长线上取一点E，使DE=DM，在E点开工就能使A、C、E成一条直线，你知道其中的道理吗？
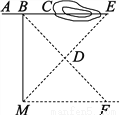
说明见解析
【解析】试题分析：首先证明≌，可得进而得到BE∥MF，再由∥MF根据过直线外一点有且只有一条直线与已知直线平行，可得A、C、E三点在一条直线上．
试题解析：
≌
∴BE∥MF，
∵AB∥MF，
根据过直线外一点有且只有一条直线与已知直线平行，
在一条直线上．
计算tan 46°≈_______ ．(精确到0.01)
1.04
【解析】试题解析：tan 46°≈1.0355303138≈1.04.
故答案为：10.4. 下列事件发生的概率为0的是( )
A. 射击运动员只射击1次,就命中靶心
B. 任取一个有理数x,都有|x|≥0
C. 画一个三角形,使其三边的长分别为8 cm,6 cm,2 cm
D. 拋掷一枚质地均匀且六个面分别刻有1到6的点数的正方体骰子,朝上一面的点数为6
C
【解析】【解析】
A．是随机事件，概率在0-1之间；
B．是必然事件，概率=1；
C．是不可能事件，概率=0；
D．是随机事件，概率在0-1之间．
故选C． 小华要设计一个摸球游戏,使得摸到红球的概率为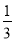
,如果设计符合要求,那么他周末就可以逛公园了,但妈妈对他的设计作出如下要求:(1)至少有四种颜色的球;
(2)至少有一个球是黄球.小华应该怎样设计呢?
答案见解析
【解析】试题分析：用6个球，其中2个红球，1个白球、1个蓝球，2个黄球，从而设计出摸球游戏．
试题解析：【解析】
用6个除颜色外完全相同的红球、白球、蓝球、黄球设计一个摸球游戏，其中2个红球，1个白球、1个蓝球，2个黄球． 一个箱子中放有红、黑、黄三种小球,每个球除颜色外都相同,三个人先后去摸球,一人摸一次,一次摸出一个小球,摸出后放回,摸出黑色小球为赢.这个游戏是( )
A. 公平的 B. 先摸者赢的可能性大 C. 不公平的 D. 后摸者赢的可能性大
A
【解析】【解析】
∵一个箱子中放有红、黄、黑三种小球，三个人先后去摸球，一人摸一次，一次摸出一个小球，摸出后放回，∴三个人摸到每种球的概率均相等，故这个游戏是公平的．故选A． 在△ABC中，AB=AC=12cm，BC=6cm，D为BC的中点，动点P从B点出发，以每秒1cm的速度沿B→A→C的方向运动，设运动时间为t，那么当t=_________秒时，过D、P两点的直线将△ABC的周长分成两个部分，使其中一部分是另一部分的2倍．
7或17
【解析】试题解析：分两种情况：
（1）P点在AB上时，如图，
∵AB=AC=12cm，BD=CD=BC=×6=3cm，
设P点运动了t秒，则BP=t，AP=12-t，由题意得：
BP+BD=（AP+AC+CD）或（BP+BD）=AP+AC+CD，
∴t+3=（12-t+12+3）①或（t+3）=12-t+12+3②，
解①得t=7秒，解②得，t=... 已知四条线段的长分别为2、3、4、5，用其中的三条线段构成的三角形的周长是_____________.
9或11或12
【解析】试题解析：由四条线段组成三角形的情况有：2，3，4；2，4，5；3，4，5，
故周长为9或11或12.
故答案为：9或11或12. 一种饮料重约300g，罐上注有“蛋白质含量≥0.5%”，其中蛋白质的含量为多少克？
不少于1.5克
【解析】
试题分析：根据“蛋白质含量≥0.5%”，即可得到结果.
300×0.5%=1.5克
答：其中蛋白质的含量不少于1.5克. 如图，点O在直线AB上，射线OC平分∠DOB．若∠COB=35°，则∠AOD等于( ).
A. 35° B. 70°
C. 110° D. 145°
C
【解析】∵OC平分∠DOB，∠COB=35°，
∴∠BOD=2∠COB=2×35°=70°,
∴∠AOD=180°-70°=110°.
故选D.