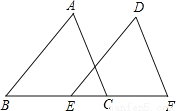
如图，点B、E、C、F在一条直线上，AB∥DE，AB=DE，BE=CF，AC=6，则DF=
6.
【解析】
试题分析：根据题中条件由SAS可得△ABC≌△DEF，根据全等三角形的性质可得AC=DF=6．
试题解析: ∵AB∥DE，
∴∠B=∠DEF
∵BE=CF，
∴BC=EF，
在△ABC和△DEF中，
，
∴△ABC≌△DEF（SAS），
∴AC=DF=6． 如图所示为农村居民住宅侧面截面图，屋坡AF、AG分别架在墙体的点B，点C处，且AB＝AC，侧面四边形BDEC为长方形．若测得∠FAG＝110°，则∠FBD＝( )
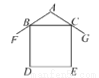
A. 35° B. 40° C. 55° D. 70°
C
【解析】在△ABC中，AB＝AC，∠BAC＝110°，根据等腰三角形的性质和三角形的内角和定理可得∠ABC=35°，由四边形BDEC为长方形可得∠DBC=90°，再由平角的定义可得∠FBD=180°-∠ABC-∠DBC=180°-35°-90°=55°，故选C. 如图，△ABC中，AB=AC,∠B=70°，则∠A的度数是（ ）
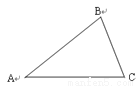
A. 70° B. 55° C. 50° D. 40°
D
【解析】试题解析：【解析】
∵AB＝AC，
∴∠B＝∠C，
∵∠B＝70°，
∴∠C＝70°，
∵∠A＋∠B＋∠C＝180°，
∴∠A＝40°.
故应选D. 如图，在△ABC中，点D在BC上，AB=AD=DC，∠B=80°，则∠C的度数为（ ）
A. 30° B. 40° C. 45° D. 60°
B
【解析】试题分析：先根据等腰三角形的性质求出∠ADB的度数，再由平角的定义得出∠ADC的度数，根据等腰三角形的性质即可得出结论．
【解析】
∵△ABD中，AB=AD，∠B=80°，
∴∠B=∠ADB=80°，
∴∠ADC=180°﹣∠ADB=100°，
∵AD=CD，
∴∠C===40°．
故选：B． 如图，AB∥CE，BF交CE于点D，DE＝DF，∠F＝20°，则∠B的度数为______．
40度
【解析】试题分析：由题可知，DE＝DF，∠F＝20°∴∠E=∠F＝20°∴∠BDE=∠E+∠F=40°，又 AB∥CE，∴∠B=∠BDE=40°，故答案为40度。 如图，AB=AC，要使△ABE≌△ACD，应添加的条件是___________.（添加一条件即可）.
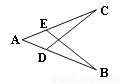
∠C=∠B（答案不唯一）
【解析】试题分析：要使△ABE≌△ACD，已知AB=AC，∠A=∠A，则可以添加一个边从而利用SAS来判定其全等，或添加一个角从而利用AAS来判定其全等．
【解析】
添加∠B=∠C或AE=AD后可分别根据ASA、SAS判定△ABE≌△ACD．
故答案为：∠B=∠C或AE=AD． 如图，在△ABC中，AB＝AC，∠ABC＝75°，E为BC延长线上一点，∠ABC与∠ACE的平分线相交于点D，则∠D的度数为( )
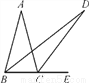
A. 15° B. 17.5° C. 20° D. 22.5°
A
【解析】因为AB＝AC，∠ABC＝75°，所以∠A=30°.
因为∠ABC与∠ACE的平分线相交于点D，所以∠ABD=∠EBD，∠ACD=∠ECD.
设ABD=∠EBD=x，∠ACD=∠ECD=y，则
2y=2x+30°①，
y=x+∠D ②
联立①②得，∠D=15°.
故选A. 如图，△ABC中，D为AB上一点，E为BC上一点，且AC=CD=BD=BE，∠A=50°，则∠CDE的度数为（ ）
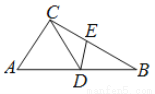
A. 50° B. 51° C. 51.5° D. 52.5°
D
【解析】试题分析：根据等腰三角形的性质推出∠A=∠CDA=50°，∠B=∠DCB，∠BDE=∠BED，根据三角形的外角性质求出∠B=25°，由三角形的内角和定理求出∠BDE=∠BED=（180°﹣25°）=77.5°，，根据平角的定义即可求出∠CDE=180°﹣∠CDA﹣∠EDB=180°﹣50°﹣77.5°=52.5°，故答案选D． 在△ABC中，如果∠B＝65°，∠A的外角等于130°，那么△ABC___(填“是”或“不是”)等腰三角形．
是
【解析】在△ABC中，∠A的外角等于130°，可得∠A=50°，又因∠B=65°，根据三角形的内角和定理可得∠C=65°，所以∠B=∠C，即可得△ABC是等腰三角形． 如图，在△ABC中，AB=AC，CD平分∠ACB，∠A=36°，则∠BDC的度数为 .
72
【解析】由AB=AC，CD平分∠ACB，∠A=36°，根据三角形内角和180°可求得∠B等于∠ACB，并能求出其角度，在△DBC求得所求角度．
【解析】
∵AB=AC，CD平分∠ACB，∠A=36°，
∴∠B=（180°-36°）÷2=72°，∠DCB=36°．
∴∠BDC=72°．
故答案为：72°