题目内容
如图,△ABC中,AB=AC,∠B=70°,则∠A的度数是( )
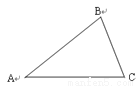
A. 70° B. 55° C. 50° D. 40°
 D
【解析】试题解析:【解析】
∵AB=AC,
∴∠B=∠C,
∵∠B=70°,
∴∠C=70°,
∵∠A+∠B+∠C=180°,
∴∠A=40°.
故应选D.
D
【解析】试题解析:【解析】
∵AB=AC,
∴∠B=∠C,
∵∠B=70°,
∴∠C=70°,
∵∠A+∠B+∠C=180°,
∴∠A=40°.
故应选D.
练习册系列答案
相关题目
如图,在Rt△ABC中,∠C=90°,AB=2BC,则sinB的值为 .
 【解析】试题分析:因为在Rt△ABC中,∠C = 90°,AB = 2BC,所以.
【解析】试题分析:因为在Rt△ABC中,∠C = 90°,AB = 2BC,所以. 如图,OC是∠AOB的平分线,P是OC上一点,PD⊥OA于点D,PD=6,则点P到边OB的距离为( )
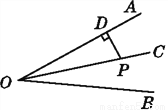
A. 6 B. 5 C. 4 D. 3
 A
【解析】试题分析:如图,过点P作PE⊥OB于点E,∵OC是∠AOB的平分线,PD⊥OA于D,∴PE=PD,∵PD=6,∴PE=6,即点P到OB的距离是6.故选A.
A
【解析】试题分析:如图,过点P作PE⊥OB于点E,∵OC是∠AOB的平分线,PD⊥OA于D,∴PE=PD,∵PD=6,∴PE=6,即点P到OB的距离是6.故选A. 如图,在△ABC中,AC=3,BC=4,AB=5,则tanB的值是( )
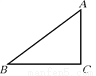
A. 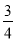 B.
B. 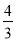 C.
C. 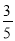 D.
D. 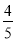
 A
【解析】试题解析:∵AC=3,BC=4,AB=5,
∴AC2+BC2=AB2,
∴∠C=90°,
∴tanB=,
故选A.
A
【解析】试题解析:∵AC=3,BC=4,AB=5,
∴AC2+BC2=AB2,
∴∠C=90°,
∴tanB=,
故选A. 如图,△ABC中,D为AB上一点,E为BC上一点,且AC=CD=BD=BE,∠A=50°,则∠CDE的度数为( )
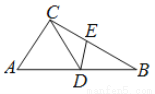
A. 50° B. 51° C. 51.5° D. 52.5°
 D
【解析】试题分析:根据等腰三角形的性质推出∠A=∠CDA=50°,∠B=∠DCB,∠BDE=∠BED,根据三角形的外角性质求出∠B=25°,由三角形的内角和定理求出∠BDE=∠BED=(180°﹣25°)=77.5°,,根据平角的定义即可求出∠CDE=180°﹣∠CDA﹣∠EDB=180°﹣50°﹣77.5°=52.5°,故答案选D.
D
【解析】试题分析:根据等腰三角形的性质推出∠A=∠CDA=50°,∠B=∠DCB,∠BDE=∠BED,根据三角形的外角性质求出∠B=25°,由三角形的内角和定理求出∠BDE=∠BED=(180°﹣25°)=77.5°,,根据平角的定义即可求出∠CDE=180°﹣∠CDA﹣∠EDB=180°﹣50°﹣77.5°=52.5°,故答案选D. 如图,已知∠ABC=∠DCB,下列所给条件不能证明△ABC≌△DCB的是( )
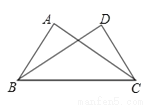
A. ∠A=∠D B. AB=DC C. ∠ACB=∠DBC D. AC=BD
 D
【解析】试题分析:根据题目所给条件∠ABC=∠DCB,再加上公共边BC=BC,然后再结合判定定理分别进行分析即可.
【解析】
A、添加∠A=∠D可利用AAS判定△ABC≌△DCB,故此选项不合题意;
B、添加AB=DC可利用SAS定理判定△ABC≌△DCB,故此选项不合题意;
C、添加∠ACB=∠DBC可利用ASA定理判定△ABC≌△DCB,故此选项不合题意;
...
D
【解析】试题分析:根据题目所给条件∠ABC=∠DCB,再加上公共边BC=BC,然后再结合判定定理分别进行分析即可.
【解析】
A、添加∠A=∠D可利用AAS判定△ABC≌△DCB,故此选项不合题意;
B、添加AB=DC可利用SAS定理判定△ABC≌△DCB,故此选项不合题意;
C、添加∠ACB=∠DBC可利用ASA定理判定△ABC≌△DCB,故此选项不合题意;
... 等腰三角形底边与底边上的高的比是2: 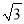 ,则顶角为( )
,则顶角为( )
A. 60° B. 90° C. 120° D. 150°
 A
【解析】如图,在△ABC中,AB=AC,AD⊥CB于D,
依题意得CD:AD=1: =:3,而tan∠DAC=CD:AD,
∴tan∠DAC=:3
∴∠DAC=30°,
∴顶角∠BAC=60°.
故选A.
A
【解析】如图,在△ABC中,AB=AC,AD⊥CB于D,
依题意得CD:AD=1: =:3,而tan∠DAC=CD:AD,
∴tan∠DAC=:3
∴∠DAC=30°,
∴顶角∠BAC=60°.
故选A. 下列事件中,是等可能事件的是_____________.(填序号)
①抛掷一枚均匀的正方体骰子一次,朝上的点数是奇数与朝上的点数是偶数;
②袋子中装有红、黄两种颜色的球,一次抽到红球与黄球;
③随意掷一枚均匀的硬币一次,正面朝上与反面朝上;
④掷一枚图钉一次,钉尖着地与钉尖朝上.
 ①③
【解析】【解析】
①抛掷一枚均匀的正方体骰子一次,朝上的点数是奇数与朝上的点数是偶数是等可能事件;
②袋子中装有红、黄两种颜色的球,一次抽到红球与黄球,因为不知道两种球的具体数量,所以不能确定是否为等可能事件;
③随意掷一枚均匀的硬币一次,正面朝上与反面朝上是等可能事件;
④掷一枚图钉一次,钉尖着地与钉尖朝上不是等可能事件.
故答案为:①③.
①③
【解析】【解析】
①抛掷一枚均匀的正方体骰子一次,朝上的点数是奇数与朝上的点数是偶数是等可能事件;
②袋子中装有红、黄两种颜色的球,一次抽到红球与黄球,因为不知道两种球的具体数量,所以不能确定是否为等可能事件;
③随意掷一枚均匀的硬币一次,正面朝上与反面朝上是等可能事件;
④掷一枚图钉一次,钉尖着地与钉尖朝上不是等可能事件.
故答案为:①③. 根据下列已知条件,能画出唯一△ABC的是( )
A. AB=3,BC=4,CA=8 B. AB=4,BC=3,∠A=30°
C. ∠A=60°,∠B=45°,AB=4 D. ∠C=90°,AB=6
 C
【解析】由一定的已知条件画三角形,要使画出的三角形是唯一的,说明不同的人根据这些条件画出的三角形一定是全等的;而由全等三角形的判定方法可知当两个三角形满足A、B、D选项中的边、角对应相等时,两个三角形不一定全等,只有满足C中的边、角对应相等时,可以由“ASA”判定两三角形全等.故选C.
C
【解析】由一定的已知条件画三角形,要使画出的三角形是唯一的,说明不同的人根据这些条件画出的三角形一定是全等的;而由全等三角形的判定方法可知当两个三角形满足A、B、D选项中的边、角对应相等时,两个三角形不一定全等,只有满足C中的边、角对应相等时,可以由“ASA”判定两三角形全等.故选C. 
