��Ŀ����
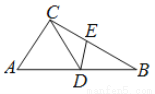
��ͼ����ABC�У�DΪAB��һ�㣬EΪBC��һ�㣬��AC=CD=BD=BE����A=50�㣬���CDE�Ķ���Ϊ�� ��
A. 50�� B. 51�� C. 51.5�� D. 52.5��
 D
��������������������ݵ��������ε������Ƴ���A=��CDA=50�㣬��B=��DCB����BDE=��BED�����������ε�������������B=25�㣬�������ε��ڽǺͶ��������BDE=��BED=��180�㩁25�㣩=77.5�㣬������ƽ�ǵĶ��弴�������CDE=180�㩁��CDA����EDB=180�㩁50�㩁77.5��=52.5�㣬�ʴ�ѡD��
D
��������������������ݵ��������ε������Ƴ���A=��CDA=50�㣬��B=��DCB����BDE=��BED�����������ε�������������B=25�㣬�������ε��ڽǺͶ��������BDE=��BED=��180�㩁25�㣩=77.5�㣬������ƽ�ǵĶ��弴�������CDE=180�㩁��CDA����EDB=180�㩁50�㩁77.5��=52.5�㣬�ʴ�ѡD��
��ϰ��ϵ�д�
 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
�����Ŀ
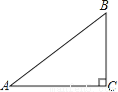
��ͼ���ڡ�ABC�У���C��90�㣬AB��5��BC��3����sinA��ֵΪ�� ��
A. 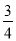 B.
B. 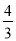 C.
C. 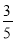 D.
D. 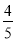
 C
�������������������Rt��ABC�У���C=90�㣬AC=3��BC=4��
�ɹ��ɶ�������
AB=��
cosA=��
��ѡA��
C
�������������������Rt��ABC�У���C=90�㣬AC=3��BC=4��
�ɹ��ɶ�������
AB=��
cosA=��
��ѡA�� ��ͼ,�ڡ�ABC��,BDƽ�֡�ABC,��AC�ڵ�D,BC������һ��E,����DE,��AD��DE�Ĺ�ϵΪ(����)
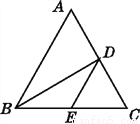
A. AD>DE B. AD=DE
C. AD<DE D. ��ȷ��
 D
�����������ݽ�ƽ�����ϵĵ㵽�ǵ����߾�����ȿɵõ�D��AB��BC�ľ�����ȣ�AD��BE�����ǵ�D��AB��BC�ľ��룬��С��ȷ����
��������
��BDƽ�֡�ABC��
���D��AB��BC�ľ�����ȣ�
��AD���ǵ�D��AB�ľ��룬��E��BC��һ�㣬
��AD��DE�Ĵ�С��ȷ��.
��ѡD.
D
�����������ݽ�ƽ�����ϵĵ㵽�ǵ����߾�����ȿɵõ�D��AB��BC�ľ�����ȣ�AD��BE�����ǵ�D��AB��BC�ľ��룬��С��ȷ����
��������
��BDƽ�֡�ABC��
���D��AB��BC�ľ�����ȣ�
��AD���ǵ�D��AB�ľ��룬��E��BC��һ�㣬
��AD��DE�Ĵ�С��ȷ��.
��ѡD. ��Rt��ABC�У�BC=3�� 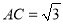 ��
�� 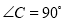 ����
����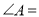 ___________��
___________��
 60��
�������������������ͼ��ʾ��
��BC=3��AC=����C=90�㣬
��tanA=��
���A=60�㣮
�ʴ�Ϊ��60�㣮
60��
�������������������ͼ��ʾ��
��BC=3��AC=����C=90�㣬
��tanA=��
���A=60�㣮
�ʴ�Ϊ��60�㣮 �ڡ�ABC�У���C��90�㣬a��5��c��17���ÿ�ѧ���������AԼ���� ( )
A. 17.6�� B. 17��6�� C. 17��16�� D. 17.16��
 A
�����������������sinA=��
A=sin-10.294=17.6�㣬
��ѡA��
A
�����������������sinA=��
A=sin-10.294=17.6�㣬
��ѡA�� ��ͼ����ABC�У�AB=AC,��B=70�㣬���A�Ķ����ǣ� ��
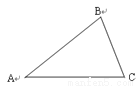
A. 70�� B. 55�� C. 50�� D. 40��
 D
�������������������������
��AB��AC��
���B����C��
�ߡ�B��70�㣬
���C��70�㣬
�ߡ�A����B����C��180�㣬
���A��40��.
��ӦѡD.
D
�������������������������
��AB��AC��
���B����C��
�ߡ�B��70�㣬
���C��70�㣬
�ߡ�A����B����C��180�㣬
���A��40��.
��ӦѡD. һ��������ľ����б���»�����ľ�们����ͼλ��ʱ��AB=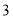 m����֪ľ���BE=
m����֪ľ���BE=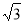 m��б�½�Ϊ30�㣬��ľ��˵�E�����AC�ĸ߶�EFΪ m��
m��б�½�Ϊ30�㣬��ľ��˵�E�����AC�ĸ߶�EFΪ m��
 3.
��������
�������������AE����Rt��ABE�����AE�����ݡ�EAB������ֵ�����EAB�Ķ������̶��õ���EAF�Ķ�������Rt��EAF�У����EF���ɵó��𰸣�
�������������AE��
��Rt��ABE��AB=3m��BE=m��
��AE=m��
�֡�tan��EAB=��
���EAB=30�㣬
��Rt��AEF�У���EAF=��EAB+��BAC=60�㣬
...
3.
��������
�������������AE����Rt��ABE�����AE�����ݡ�EAB������ֵ�����EAB�Ķ������̶��õ���EAF�Ķ�������Rt��EAF�У����EF���ɵó��𰸣�
�������������AE��
��Rt��ABE��AB=3m��BE=m��
��AE=m��
�֡�tan��EAB=��
���EAB=30�㣬
��Rt��AEF�У���EAF=��EAB+��BAC=60�㣬
... һ������������װ��1������2������3���������dz���ɫ�ⶼ��ͬ��������������һ�����Ǻ���ĸ���Ϊ(�� ��)
A.  B.
B.  C.
C.  D.
D. 
 C
���������������������36�ֵȿ��ܵĽ����������������������ǡΪ����Ľ����Ϊ6��
����������������ǡΪ����ĸ���=��
C
���������������������36�ֵȿ��ܵĽ����������������������ǡΪ����Ľ����Ϊ6��
����������������ǡΪ����ĸ���=�� ��ͼ����1=��2��Ҫʹ��ABD�ա�ACD�������ӵ�һ��������_________
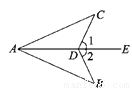
 ��B=��C��
����������������������ӵ�һ�������ǣ���B=��C��
���ɣ��ߡ�1=��2��
���ADC=��ADB��
�ڡ�ABD�͡�ACD�У�
���ABD�ա�ACD(AAS).
�ʴ�Ϊ����B=��C.(�𰸲�Ψһ).
��B=��C��
����������������������ӵ�һ�������ǣ���B=��C��
���ɣ��ߡ�1=��2��
���ADC=��ADB��
�ڡ�ABD�͡�ACD�У�
���ABD�ա�ACD(AAS).
�ʴ�Ϊ����B=��C.(�𰸲�Ψһ). 
