题目内容
如图，AB∥CE，BF交CE于点D，DE＝DF，∠F＝20°，则∠B的度数为______．
40度
【解析】试题分析：由题可知，DE＝DF，∠F＝20°∴∠E=∠F＝20°∴∠BDE=∠E+∠F=40°，又 AB∥CE，∴∠B=∠BDE=40°，故答案为40度。
练习册系列答案
备战中考寒假系列答案
相关题目
如图，每个小正方形的边长为1，A、B、C是小正方形的顶点，则∠ABC的正弦值为 ．
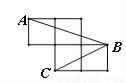
【解析】
试题分析：本题首先将∠ABC转化到某一个直角三角形中，然后进行求值. 如图，OP平分∠AOB，PA⊥OA,PB⊥OB，垂足分别为A，B。下列结论中不一定成立的是（ ）
A、PA=PB B、PO平分∠AOB
C、OA=OB D、AB垂直平分OP
D
【解析】
试题分析：本题要从已知条件OP平分∠AOB入手，利用角平分线的性质：因OP平分∠AOB，PA⊥OA，PB⊥OB，得到PA=PB，进而推出△AOE≌△BOE，从未得到∠APO=∠BPO，OA=OB，因此A、B、C项正确；设PO与AB相交于E，由OA=OB，∠AOP=∠BOP，OE=OE，得证△AOE≌△BOE，进而得∠AEO=∠BEO=90°，因此得证OP垂直AB，而不能得... 如图，已知正方形ABCD的边长为2，如果将线段BD绕着点B旋转后，点D落在CB的延长线上的点
处，那么tan∠BAD′等于（ ）
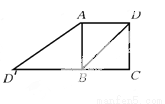
A. 1 B.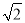 
C. 
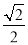D.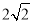 
B
【解析】试题解析：正方形ABCD的边长为2，则对角线BD=．
∴BD′=BD=．
∴tan∠BAD’=．
故选B. 如图，在△ABC中，AB=AC，CD平分∠ACB，∠A=36°，则∠BDC的度数为 .
72
【解析】由AB=AC，CD平分∠ACB，∠A=36°，根据三角形内角和180°可求得∠B等于∠ACB，并能求出其角度，在△DBC求得所求角度．
【解析】
∵AB=AC，CD平分∠ACB，∠A=36°，
∴∠B=（180°-36°）÷2=72°，∠DCB=36°．
∴∠BDC=72°．
故答案为：72° 如图所示，F、C在线段BE上，且∠1＝∠2，BC＝EF.若要根据“SAS”使△ABC≌△DEF，还需要补充的条件是________.
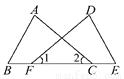
AC＝DF
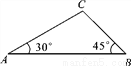
【解析】已知∠1＝∠2，BC＝EF，根据“SAS”使△ABC≌△DEF，还需要补充的条件是AC＝DF. 如图，在△ABC中，∠A＝30°，∠B＝45°，AC＝2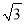
，则AB的长为_______．
3＋
【解析】过C作CD⊥AB于D，∴∠ADC＝∠BDC＝90°．∵∠B＝45°，∴∠BCD＝∠B＝45°，
∴CD＝BD．∵∠A＝30°，，∴，∴．
由勾股定理得： ，∴． （3分）必然事件的概率是（ ）
A．﹣1 B．0 C．0.5 D．1
D．
【解析】
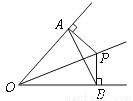
试题分析：∵必然事件就是一定发生的事件，∴必然事件发生的概率是1．故选D． 如图所示，在△ABC中，AQ=PQ，PR=PS，PR⊥AB于R，PS⊥AC于S，则下列三个结论：①AS=AR；②QP∥AR；③△BPR≌△QPS中（ ）
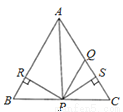
A. 全部正确 B. 仅①和②正确 C. 仅①正确 D. 仅①和③正确
B
【解析】∵PR=PS，PR⊥AB于R，PS⊥AC于S，
∴∠PAB=∠PAC，∠PSA=∠PRA=90°，
在△PAR和△PAS中，
，
∴△PAR≌△PAS（AAS），
∴AR=AS，∴①正确；
∵AQ=PQ，
∠CAP=∠APQ，
∵∠CAP=∠BAP，
∴∠BAP=∠APQ，
∴PQ∥AB，∴②正确；
∵PR⊥AB，...