题目内容
如图,在△ABC中,点D在BC上,AB=AD=DC,∠B=80°,则∠C的度数为( )

A. 30° B. 40° C. 45° D. 60°
 B
【解析】试题分析:先根据等腰三角形的性质求出∠ADB的度数,再由平角的定义得出∠ADC的度数,根据等腰三角形的性质即可得出结论.
【解析】
∵△ABD中,AB=AD,∠B=80°,
∴∠B=∠ADB=80°,
∴∠ADC=180°﹣∠ADB=100°,
∵AD=CD,
∴∠C===40°.
故选:B.
B
【解析】试题分析:先根据等腰三角形的性质求出∠ADB的度数,再由平角的定义得出∠ADC的度数,根据等腰三角形的性质即可得出结论.
【解析】
∵△ABD中,AB=AD,∠B=80°,
∴∠B=∠ADB=80°,
∴∠ADC=180°﹣∠ADB=100°,
∵AD=CD,
∴∠C===40°.
故选:B.
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案在Rt△ABC中,∠C=90°,CD是斜边AB上的高,如果CD=3,BD=2.求cos∠A的值.
 【解析】分析:根据题意画出图形,进而利用锐角三角函数关系得出cosA=cos∠BCD进而求出即可.
本题解析:
如图所示:
∵∠ACB=90°,∴∠B+∠A=90°,
∵CD⊥AB,∴∠CDA=90°,∴∠B+∠BCD=90°,∴∠BCD=∠A,
∵CD=3,BD=2,∴BC=
∴cosA=cos∠BCD=
故答案为:
【解析】分析:根据题意画出图形,进而利用锐角三角函数关系得出cosA=cos∠BCD进而求出即可.
本题解析:
如图所示:
∵∠ACB=90°,∴∠B+∠A=90°,
∵CD⊥AB,∴∠CDA=90°,∴∠B+∠BCD=90°,∴∠BCD=∠A,
∵CD=3,BD=2,∴BC=
∴cosA=cos∠BCD=
故答案为: 如图,OP为∠AOB的角平分线,PC⊥OA,PD⊥OB,垂足分别是C、D,则下列结论错误的是( )
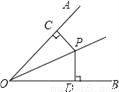
A. PC=PD B. ∠CPD=∠DOP C. ∠CPO=∠DPO D. OC=OD
 B
【解析】试题分析:已知OP为∠AOB的角平分线,PC⊥OA,PD⊥OB,垂足分别是C、D,根据角平分线的性质可得PC=PD,A正确;在Rt△OCP与Rt△ODP中,OP=OP,PC=PD,由HL可判定△OCP≌△ODP,根据全等三角形的性质可得∠CPO=∠DPO,OC=OD,故C、D正确.不能得出∠CPD=∠DOP,故B错误.故答案选B.
B
【解析】试题分析:已知OP为∠AOB的角平分线,PC⊥OA,PD⊥OB,垂足分别是C、D,根据角平分线的性质可得PC=PD,A正确;在Rt△OCP与Rt△ODP中,OP=OP,PC=PD,由HL可判定△OCP≌△ODP,根据全等三角形的性质可得∠CPO=∠DPO,OC=OD,故C、D正确.不能得出∠CPD=∠DOP,故B错误.故答案选B. 在Rt△ABC中,∠C=90°,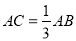 ,则cosA等于( )
,则cosA等于( )
A. 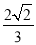 B.
B. 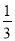 C.
C. 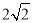 D.
D. 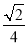
 B
【解析】试题解析:如图所示:
∵,
∴cosA=.
故选B.
B
【解析】试题解析:如图所示:
∵,
∴cosA=.
故选B. 在△ABC中,如果∠B=65°,∠A的外角等于130°,那么△ABC___(填“是”或“不是”)等腰三角形.
 是
【解析】在△ABC中,∠A的外角等于130°,可得∠A=50°,又因∠B=65°,根据三角形的内角和定理可得∠C=65°,所以∠B=∠C,即可得△ABC是等腰三角形.
是
【解析】在△ABC中,∠A的外角等于130°,可得∠A=50°,又因∠B=65°,根据三角形的内角和定理可得∠C=65°,所以∠B=∠C,即可得△ABC是等腰三角形. 如图所示,BA⊥CA,AB∥CD,AB=CE,AC=CD,则△ABC≌______,理由是_____,所以∠ABC=______,∠ACB=______,由此可知BC与DE的位置关系为__________.
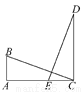
 △CED SAS ∠CED ∠CDE 互相垂直
【解析】∵BA⊥CA,
∴∠BAC=90°,
∵AB∥CD,
∴∠ACD=∠BAC=90°,
在△ACB和△CDE中,
,
∴△ABC≌△ECD(SAS),
∴∠ABC=∠CED,∠ACB=∠CDE,
又因∠ACB+∠BCD=90°,
∴∠CDE+∠BCD=90°,
∴BC⊥DE.
...
△CED SAS ∠CED ∠CDE 互相垂直
【解析】∵BA⊥CA,
∴∠BAC=90°,
∵AB∥CD,
∴∠ACD=∠BAC=90°,
在△ACB和△CDE中,
,
∴△ABC≌△ECD(SAS),
∴∠ABC=∠CED,∠ACB=∠CDE,
又因∠ACB+∠BCD=90°,
∴∠CDE+∠BCD=90°,
∴BC⊥DE.
... △ABC中,∠B=90°,AC=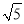 ,tan∠C=
,tan∠C=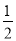 ,则BC边的长为( )
,则BC边的长为( )
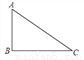
A. 2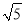 B. 2 C.
B. 2 C. 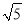 D. 4
D. 4
 B
【解析】∵∠B=90°,
∴tan∠C==,
设AB=x,则BC=2x,
∴AC==x,
∴x=,解得x=1,
∴BC=2x=2.
故选B.
B
【解析】∵∠B=90°,
∴tan∠C==,
设AB=x,则BC=2x,
∴AC==x,
∴x=,解得x=1,
∴BC=2x=2.
故选B. (1)必然事件A的概率为:P(A)=______________.
(2)不可能事件A的概率为:P(A)=______________.
(3)随机事件A的概率为P(A):______________.
(4)随机事件的概率的规律:事件发生的可能性越大,则它的概率越接近于_____________;反之,事件发生的可能性越小,则它的概率越接近于_____________.从1~9这九个自然数中任取一个,是2的倍数的概率是_____________.方程5x=10的解为负数的概率是_____________.
 1, 0, 0
1, 0, 0在两个三角形中给出条件:①两角一边对应相等;②两边一角对应相等;③两角夹边对应相等;④两边夹角对应相等;⑤三边对应相等;⑥三角形对应相等.其中能判断出三角形全等的是( )
A. ①②③⑤ B. ①③④⑤
C. ①④⑤⑥ D. ②③④⑤
 B
【解析】试题解析:①正确,符合AAS;
②不正确,该角应该是两边的夹角;
③正确,符合ASA;
④正确,符合SAS;
⑤正确,符合SSS;
⑥不正确,判定三角形全等必须有边的参与.
故选B.
B
【解析】试题解析:①正确,符合AAS;
②不正确,该角应该是两边的夹角;
③正确,符合ASA;
④正确,符合SAS;
⑤正确,符合SSS;
⑥不正确,判定三角形全等必须有边的参与.
故选B. 
