在△ABC中,AB=AC,且BC=8cm,BD是腰AC的中线,△ABC的周长分为两部分,已知它们的差为2cm,则等腰三角形的腰长为__________.
 10cm或6cm
【解析】如图∵BD是腰AC的中线,
∴AD=CD,
①当△ABD的周长与△BCD的周长差为2时,即AB+AD+BD-(BD+BC+CD)=2,
∴AB-BC=2,
∵BC=8cm,
∴AB=10cm.
②当△BCD的周长与△ABD的周长差为2时,即BD+BC+CD -(AB+AD+BD)=2,
∴BC - AB =2,
∵BC...
10cm或6cm
【解析】如图∵BD是腰AC的中线,
∴AD=CD,
①当△ABD的周长与△BCD的周长差为2时,即AB+AD+BD-(BD+BC+CD)=2,
∴AB-BC=2,
∵BC=8cm,
∴AB=10cm.
②当△BCD的周长与△ABD的周长差为2时,即BD+BC+CD -(AB+AD+BD)=2,
∴BC - AB =2,
∵BC... 如图,点D,E在△ABC的边BC上,AB=AC,BD=CE.
求证:AD=AE.
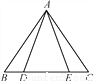
 证明见解析
【解析】试题分析:利用等腰三角形的性质得到∠B=∠C,然后证明△ABD≌△ACE即可证得结论.
【解答】证明:∵AB=AC,
∴∠B=∠C,
在△ABD与△ACE中,
∵,
∴△ABD≌△ACE(SAS),
∴AD=AE.
证明见解析
【解析】试题分析:利用等腰三角形的性质得到∠B=∠C,然后证明△ABD≌△ACE即可证得结论.
【解答】证明:∵AB=AC,
∴∠B=∠C,
在△ABD与△ACE中,
∵,
∴△ABD≌△ACE(SAS),
∴AD=AE. 在△ABC中,∠C=90°,a=5,c=17,用科学计算器求∠A约等于 ( )
A. 17.6° B. 17°6′ C. 17°16′ D. 17.16°
 A
【解析】试题解析:sinA=,
A=sin-10.294=17.6°,
故选A.
A
【解析】试题解析:sinA=,
A=sin-10.294=17.6°,
故选A. 一个直角三角形有两条边长为3,4,则较小的锐角约为( )
A. 37° B. 41° C. 37°或41° D. 以上答案均不对
 C
【解析】试题解析:①若3、4是直角边,
∵两直角边为3,4,
∴斜边长==5,
∴较小的锐角所对的直角边为3,则其正弦值为;
②若斜边长为4,则较小边=≈2.65,
∴较小边所对锐角正弦值约==0.6625,
利用计算器求得角约为37°或41°.
故选C.
C
【解析】试题解析:①若3、4是直角边,
∵两直角边为3,4,
∴斜边长==5,
∴较小的锐角所对的直角边为3,则其正弦值为;
②若斜边长为4,则较小边=≈2.65,
∴较小边所对锐角正弦值约==0.6625,
利用计算器求得角约为37°或41°.
故选C. 如图,在△ABC中,AC=3,BC=4,AB=5,则tanB的值是( )
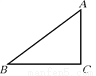
A. 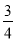 B.
B. 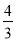 C.
C. 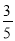 D.
D. 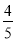
 A
【解析】试题解析:∵AC=3,BC=4,AB=5,
∴AC2+BC2=AB2,
∴∠C=90°,
∴tanB=,
故选A.
A
【解析】试题解析:∵AC=3,BC=4,AB=5,
∴AC2+BC2=AB2,
∴∠C=90°,
∴tanB=,
故选A. 在Rt△ABC中,∠C=90°,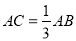 ,则cosA等于( )
,则cosA等于( )
A. 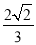 B.
B. 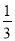 C.
C. 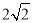 D.
D. 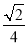
 B
【解析】试题解析:如图所示:
∵,
∴cosA=.
故选B.
B
【解析】试题解析:如图所示:
∵,
∴cosA=.
故选B. 如图,已知正方形ABCD的边长为2,如果将线段BD绕着点B旋转后,点D落在CB的延长线上的点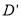 处,那么tan∠BAD′等于( )
处,那么tan∠BAD′等于( )
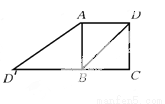
A. 1 B. 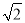 C.
C. 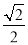 D.
D. 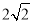
 B
【解析】试题解析:正方形ABCD的边长为2,则对角线BD=.
∴BD′=BD=.
∴tan∠BAD’=.
故选B.
B
【解析】试题解析:正方形ABCD的边长为2,则对角线BD=.
∴BD′=BD=.
∴tan∠BAD’=.
故选B. 计算tan 46°≈_______ .(精确到0.01)
 1.04
【解析】试题解析:tan 46°≈1.0355303138≈1.04.
故答案为:10.4.
1.04
【解析】试题解析:tan 46°≈1.0355303138≈1.04.
故答案为:10.4. 在△ABC中,∠C-90°,若tanB=2,a=1,则b=________.
 2
【解析】试题解析:在Rt△ABC中,
∵∠C=90°,
∴AB为斜边.
∴b=AC•tanB
=a•tanB
=2.
故答案为:2.
2
【解析】试题解析:在Rt△ABC中,
∵∠C=90°,
∴AB为斜边.
∴b=AC•tanB
=a•tanB
=2.
故答案为:2. 在Rt△ABC中,BC=3, 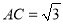 ,
, 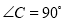 ,则
,则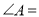 ___________.
___________.
 60°
【解析】试题解析:如图所示:
∵BC=3,AC=,∠C=90°,
∴tanA=,
∴∠A=60°.
故答案为:60°.
60°
【解析】试题解析:如图所示:
∵BC=3,AC=,∠C=90°,
∴tanA=,
∴∠A=60°.
故答案为:60°.