题目内容
如图，已知正方形ABCD的边长为2，如果将线段BD绕着点B旋转后，点D落在CB的延长线上的点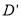
处，那么tan∠BAD′等于（ ）
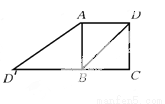
A. 1 B.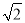 
C. 
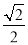D.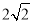 
B
【解析】试题解析：正方形ABCD的边长为2，则对角线BD=．
∴BD′=BD=．
∴tan∠BAD’=．
故选B.
练习册系列答案
阅读快车系列答案
相关题目
在Rt△ABC中，如果各边长度都扩大为原来的2倍，那么锐角A的正弦值（ ）
A. 扩大2倍 B. 缩小2倍 C. 扩大4倍 D. 没有变化
D
【解析】根据锐角三角函数的概念，知若各边长都扩大2倍，则sinA的值不变．
故选D． 某电视台“走基层”栏目的一位记者乘汽车赴360km外的农村采访，全程的前一部分为高速公路，后一部分为乡村公路，若汽车在高速公路和乡村公路上分别以某一速度匀速行驶，汽车行驶的路程y（单位：km）与时间x（单位：h）之间的关系如图所示，则下列结论正确的是
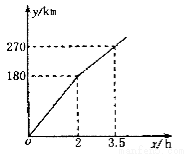
A. 汽车在高速公路上行驶速度为100km／h
B. 乡村公路总长为90km
C. 汽车在乡村公路上行驶速度为60km／h
D. 该记者在出发后4.5h到达采访地
C
【解析】
试题分析：若汽车在高速公路和乡村公路上分别以某一速度匀速行驶，由图得汽车在高速公路上行驶速度为，所以A错误；乡村公路总长=360km-180km=180km,所以B错误；汽车在乡村公路上行驶速度，所以C正确；该记者在出发后到达采访地的时间=在高速公路和乡村公路上行驶时间之和=2+=2+3=5 用直尺和圆规作一个角的平分线如图所示，说明∠AOC＝∠BOC的依据是( )．
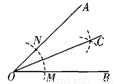
A. SSS B. ASA C. AAS D. 角平分线上的点到角两边距离相等
A
【解析】试题分析：连接NC，MC，根据SSS证△ONC≌△OMC，即可推出答案．
连接NC，MC，在△ONC和△OMC中，
∴△ONC≌△OMC（SSS）， ∴∠AOC=∠BOC 在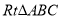
中， 
， 
， 
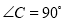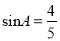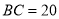，则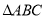
的面积为________．
150
【解析】试题解析：∵在Rt△ABC中，∠C=90°，sinA=，
∴AB=，
∴AC=，
则△ABC的面积为： AC•BC=×15×20=150．
故答案为：150． 如图，点D，E在△ABC的边BC上，AB＝AC，BD＝CE.
求证：AD＝AE.
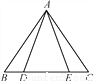
证明见解析
【解析】试题分析：利用等腰三角形的性质得到∠B=∠C，然后证明△ABD≌△ACE即可证得结论．
【解答】证明：∵AB=AC，
∴∠B=∠C，
在△ABD与△ACE中，
∵，
∴△ABD≌△ACE（SAS），
∴AD=AE． 如图，AB∥CE，BF交CE于点D，DE＝DF，∠F＝20°，则∠B的度数为______．
40度
【解析】试题分析：由题可知，DE＝DF，∠F＝20°∴∠E=∠F＝20°∴∠BDE=∠E+∠F=40°，又 AB∥CE，∴∠B=∠BDE=40°，故答案为40度。 如图,巳知A点坐标为(5,0),直线y=x+b(b＞0)与y轴交于B,连AB,∠α=75°,则b值为（ ）
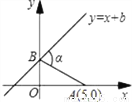
A. 3 B. 
C. 4 D. 
B
【解析】因为直线的解析式是y=x+b，
∴OB=OC=b,则∠BCA=45°；
又∵∠α=75°=∠BCA+∠BAC=45°+∠BAC(外角定理)
∴∠BAC=30°；
而点A的坐标是(5,0)，
∴OA=5，
在Rt△BAO中,∠BAC=30°，OA=5，
∴tan∠BAO=
∴BO=,即b=.
故选B. 如图，在△ABC和△CED中，AB∥CD，AB=CE，AC=CD.求证：∠B=∠E.
证明见解析.
【解析】试题分析：根据AB//CD得出∠DCA=∠CAB，结合AB=CE，AC=CD得出△CAB≌△DCE，从而得出答案.
试题解析：∵AB//CD，∴∠DCA=∠CAB 又∵AB=CE，AC=CD，∴△CAB≌△DCE ∴∠B=∠E.