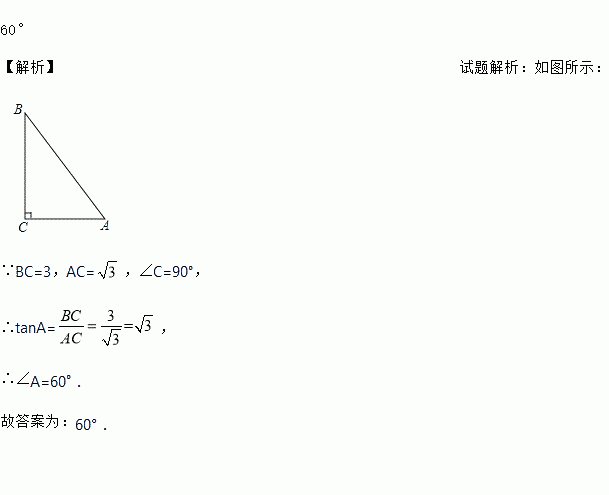题目内容
在Rt△ABC中,BC=3, 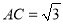 ,
, 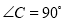 ,则
,则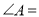 ___________.
___________.
 60°
【解析】试题解析:如图所示:
∵BC=3,AC=,∠C=90°,
∴tanA=,
∴∠A=60°.
故答案为:60°.
60°
【解析】试题解析:如图所示:
∵BC=3,AC=,∠C=90°,
∴tanA=,
∴∠A=60°.
故答案为:60°.
练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
在Rt△ABC中,∠C=90°,BC=3,AC=4,那么cos A的值等于 .
 .
【解析】
试题分析:∵在Rt△ABC中,∠C=90°,AC=4,BC=3,∴AB==,∴cosA==,故答案为:.
.
【解析】
试题分析:∵在Rt△ABC中,∠C=90°,AC=4,BC=3,∴AB==,∴cosA==,故答案为:. 某市出租车收费与行驶路程关系如图所示.如果小明姥姥乘出租车去小明家花去了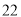 元,那么小明始姥乘车路程为__________千米.
元,那么小明始姥乘车路程为__________千米.

 13
【解析】设AB的解析式为y=kx+b,由题意,得,解得: ,
∴直线AB的解析式为y=1.6x+1.2(x≥3),
当y=22时,22=1.6x+1.2,解得:x=13,
故答案为:13.
13
【解析】设AB的解析式为y=kx+b,由题意,得,解得: ,
∴直线AB的解析式为y=1.6x+1.2(x≥3),
当y=22时,22=1.6x+1.2,解得:x=13,
故答案为:13. 如图,OC是∠AOB的平分线,P是OC上一点,PD⊥OA于点D,PD=6,则点P到边OB的距离为( )
A. 6 B. 5 C. 4 D. 3
 A
【解析】试题分析:如图,过点P作PE⊥OB于点E,∵OC是∠AOB的平分线,PD⊥OA于D,∴PE=PD,∵PD=6,∴PE=6,即点P到OB的距离是6.故选A.
A
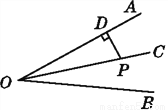
【解析】试题分析:如图,过点P作PE⊥OB于点E,∵OC是∠AOB的平分线,PD⊥OA于D,∴PE=PD,∵PD=6,∴PE=6,即点P到OB的距离是6.故选A. 如图所示,一测量员站在岸边的A处,刚好正对河岸另一边B处的一棵大树,这位测量员沿河岸向右走了50 m到达C处,在C处测得∠ACB=38°,求河的宽度.(精确到0.01 m,tan 38°≈0.7813)
 39.07
【解析】试题分析:在直角三角形中,根据已知条件利用所给角的正切值求得AB即可.
试题解析:在Rt△BAC中,∠ACB=38°.
则AB=AC•tan38°≈50×0.7813=39.065≈39.07(米).
答:河的宽度约为39.07米.
39.07
【解析】试题分析:在直角三角形中,根据已知条件利用所给角的正切值求得AB即可.
试题解析:在Rt△BAC中,∠ACB=38°.
则AB=AC•tan38°≈50×0.7813=39.065≈39.07(米).
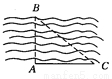
答:河的宽度约为39.07米. 如图,在△ABC中,AC=3,BC=4,AB=5,则tanB的值是( )
A. 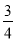 B.
B. 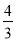 C.
C. 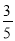 D.
D. 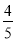
 A
【解析】试题解析:∵AC=3,BC=4,AB=5,
∴AC2+BC2=AB2,
∴∠C=90°,
∴tanB=,
故选A.
A
【解析】试题解析:∵AC=3,BC=4,AB=5,
∴AC2+BC2=AB2,
∴∠C=90°,
∴tanB=,
故选A. 如图,△ABC中,D为AB上一点,E为BC上一点,且AC=CD=BD=BE,∠A=50°,则∠CDE的度数为( )
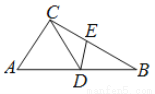
A. 50° B. 51° C. 51.5° D. 52.5°
 D
【解析】试题分析:根据等腰三角形的性质推出∠A=∠CDA=50°,∠B=∠DCB,∠BDE=∠BED,根据三角形的外角性质求出∠B=25°,由三角形的内角和定理求出∠BDE=∠BED=(180°﹣25°)=77.5°,,根据平角的定义即可求出∠CDE=180°﹣∠CDA﹣∠EDB=180°﹣50°﹣77.5°=52.5°,故答案选D.
D
【解析】试题分析:根据等腰三角形的性质推出∠A=∠CDA=50°,∠B=∠DCB,∠BDE=∠BED,根据三角形的外角性质求出∠B=25°,由三角形的内角和定理求出∠BDE=∠BED=(180°﹣25°)=77.5°,,根据平角的定义即可求出∠CDE=180°﹣∠CDA﹣∠EDB=180°﹣50°﹣77.5°=52.5°,故答案选D. 等腰三角形底边与底边上的高的比是2: 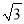 ,则顶角为( )
,则顶角为( )
A. 60° B. 90° C. 120° D. 150°
 A
【解析】如图,在△ABC中,AB=AC,AD⊥CB于D,
依题意得CD:AD=1: =:3,而tan∠DAC=CD:AD,
∴tan∠DAC=:3
∴∠DAC=30°,
∴顶角∠BAC=60°.
故选A.
A
【解析】如图,在△ABC中,AB=AC,AD⊥CB于D,
依题意得CD:AD=1: =:3,而tan∠DAC=CD:AD,
∴tan∠DAC=:3
∴∠DAC=30°,
∴顶角∠BAC=60°.
故选A. 在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E.
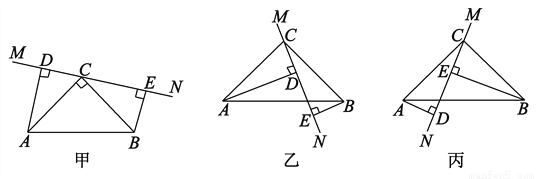
(1)当直线MN绕点C旋转到图甲的位置时,试说明:①△ADC≌△CEB;②DE=AD+BE;
(2)当直线MN绕点C旋转到图乙的位置时,试说明:DE=AD-BE;
(3)当直线MN绕点C旋转到图丙的位置时,试问DE、AD、BE具有怎样的等量关系?请写出这个等量关系,并加以证明.
 (1)证明见解析;()证明见解析;(3)AD、DE、BE所满足的等量关系是DE=BE-AD(或AD=BE-DE,BE=AD+DE等)理由见解析.
【解析】试题分析:(1)由∠ACB=90°,得∠BCE+∠ACD=90°,而AD⊥MN于D,BE⊥MN于E.则∠ADC=∠CEB=90°,根据等角的余角相等得到∠ACD=∠CBE.,易得
Rt△ADC≌Rt△CEB,所以AD=CE,DC=BE...
(1)证明见解析;()证明见解析;(3)AD、DE、BE所满足的等量关系是DE=BE-AD(或AD=BE-DE,BE=AD+DE等)理由见解析.
【解析】试题分析:(1)由∠ACB=90°,得∠BCE+∠ACD=90°,而AD⊥MN于D,BE⊥MN于E.则∠ADC=∠CEB=90°,根据等角的余角相等得到∠ACD=∠CBE.,易得
Rt△ADC≌Rt△CEB,所以AD=CE,DC=BE...