题目内容
在△ABC中,∠C-90°,若tanB=2,a=1,则b=________.
 2
【解析】试题解析:在Rt△ABC中,
∵∠C=90°,
∴AB为斜边.
∴b=AC•tanB
=a•tanB
=2.
故答案为:2.
2
【解析】试题解析:在Rt△ABC中,
∵∠C=90°,
∴AB为斜边.
∴b=AC•tanB
=a•tanB
=2.
故答案为:2.
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案如图,将∠AOB放在边长为1的小正方形组成的网格中,则tan∠AOB= .
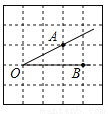
 .
【解析】试题分析:过点A作AD⊥OB垂足为D,如图,在直角△ABD中,AD=1,OD=2,则tan∠AOB==.故答案为: .
.
【解析】试题分析:过点A作AD⊥OB垂足为D,如图,在直角△ABD中,AD=1,OD=2,则tan∠AOB==.故答案为: . 小明从家跑步到学校,接着马上原路步行回家.如图是小明离家的路程y(米)与时间t(分)的函数图象,则小明回家的速度是每分钟步行 米.
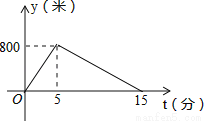
 80
【解析】
试题分析:先分析出小明家距学校800米,小明从学校步行回家的时间是15﹣5=10(分),再根据路程、时间、速度的关系即可求得.
【解析】
通过读图可知:小明家距学校800米,小明从学校步行回家的时间是15﹣5=10(分),
所以小明回家的速度是每分钟步行800÷10=80(米).
故答案为:80.
80
【解析】
试题分析:先分析出小明家距学校800米,小明从学校步行回家的时间是15﹣5=10(分),再根据路程、时间、速度的关系即可求得.
【解析】
通过读图可知:小明家距学校800米,小明从学校步行回家的时间是15﹣5=10(分),
所以小明回家的速度是每分钟步行800÷10=80(米).
故答案为:80. 根据图中尺规作图的痕迹,先判断得出结论:__________,并说明理由.
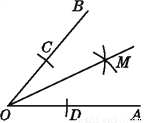
 OM平分∠BOA
【解析】根据全等三角形的判定及性质即可得出结论.
【解析】
如图所示,连接CM,DM,
由作图的痕迹可知,OC=OD,CM=DM.
又因为OM=OM,
所以△COM≌△DOM.
所以∠COM=∠DOM.
所以OM平分∠BOA.
故答案为:OM平分∠BOA.
OM平分∠BOA
【解析】根据全等三角形的判定及性质即可得出结论.
【解析】
如图所示,连接CM,DM,
由作图的痕迹可知,OC=OD,CM=DM.
又因为OM=OM,
所以△COM≌△DOM.
所以∠COM=∠DOM.
所以OM平分∠BOA.
故答案为:OM平分∠BOA. 如图,学校的保管室里,有一架5米长的梯子斜靠在墙上,此时梯子与地面所成的角为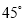 ,如果梯子的底端
,如果梯子的底端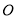 固定不动,顶端靠在对面墙上,此时梯子与地面所成的角为
固定不动,顶端靠在对面墙上,此时梯子与地面所成的角为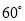 ,求此保管室的宽度
,求此保管室的宽度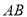 的长.
的长.
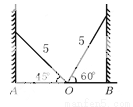
 【解析】由于两边的墙都和地面垂直,所以构成了两个直角三角形.
∵cos45°==,∴;而cos60°==,∴BO=.
∴AB=AO+BO==.
【解析】由于两边的墙都和地面垂直,所以构成了两个直角三角形.
∵cos45°==,∴;而cos60°==,∴BO=.
∴AB=AO+BO==. 一个直角三角形有两条边长为3,4,则较小的锐角约为( )
A. 37° B. 41° C. 37°或41° D. 以上答案均不对
 C
【解析】试题解析:①若3、4是直角边,
∵两直角边为3,4,
∴斜边长==5,
∴较小的锐角所对的直角边为3,则其正弦值为;
②若斜边长为4,则较小边=≈2.65,
∴较小边所对锐角正弦值约==0.6625,
利用计算器求得角约为37°或41°.
故选C.
C
【解析】试题解析:①若3、4是直角边,
∵两直角边为3,4,
∴斜边长==5,
∴较小的锐角所对的直角边为3,则其正弦值为;
②若斜边长为4,则较小边=≈2.65,
∴较小边所对锐角正弦值约==0.6625,
利用计算器求得角约为37°或41°.
故选C. 如图,在△ABC中,AB=AC,∠ABC=75°,E为BC延长线上一点,∠ABC与∠ACE的平分线相交于点D,则∠D的度数为( )
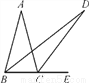
A. 15° B. 17.5° C. 20° D. 22.5°
 A
【解析】因为AB=AC,∠ABC=75°,所以∠A=30°.
因为∠ABC与∠ACE的平分线相交于点D,所以∠ABD=∠EBD,∠ACD=∠ECD.
设ABD=∠EBD=x,∠ACD=∠ECD=y,则
2y=2x+30°①,
y=x+∠D ②
联立①②得,∠D=15°.
故选A.
A
【解析】因为AB=AC,∠ABC=75°,所以∠A=30°.
因为∠ABC与∠ACE的平分线相交于点D,所以∠ABD=∠EBD,∠ACD=∠ECD.
设ABD=∠EBD=x,∠ACD=∠ECD=y,则
2y=2x+30°①,
y=x+∠D ②
联立①②得,∠D=15°.
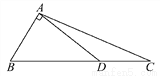
故选A. 如图,在直角△BAD中,延长斜边BD到点C,使DC=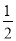 BD,连接AC,若tanB=
BD,连接AC,若tanB=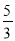 ,则tan∠CAD的值( )
,则tan∠CAD的值( )
A. 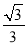 B.
B. 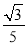 C.
C. 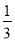 D.
D. 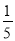
 D
【解析】试题分析:如图,延长AD,过点C作CE⊥AD,垂足为E,
∵tanB=,即,
∴设AD=5x,则AB=3x,
∵∠CDE=∠BDA,∠CED=∠BAD,
∴△CDE∽△BDA,
∴,
∴CE=x,DE= ,
∴AE= ,
∴tan∠CAD=.
故选D.
D
【解析】试题分析:如图,延长AD,过点C作CE⊥AD,垂足为E,
∵tanB=,即,
∴设AD=5x,则AB=3x,
∵∠CDE=∠BDA,∠CED=∠BAD,
∴△CDE∽△BDA,
∴,
∴CE=x,DE= ,
∴AE= ,
∴tan∠CAD=.
故选D. 如图所示,已知B、E分别是线段AC、DF的中点,AC=DF,BF交CD于点H,AE交CD于点G,CH=HG=DG,BH=GE.
(1)填空:因为B、E分别是线段AC、DF的中点,所以CB=________AC,DE=________DF.因为AC=DF,所以CB=________.在△CBH和△DEG中,因为CB=________,CH=________,BH=________EG,所以________≌________(SSS).
(2)除了(1)中的全等三角形外,请你再写出另外一对全等三角形,并说明理由.

 (1) , ,DE,DE,DG,△CBH,△DEG. (2)证明见解析.
【解析】试题分析:(1)因为B是AC的中点, 同理因为AC=DF,由上知根据上面求得: 即可得△CBH≌△DEG.两个三角形对应的三边相等,则两个三角形全等,所以找出三角形对应的三边
(2)根据题中条件分析,再用SAS来证明即可
试题解析:(1)因为B是AC的中点, 同理
因为AC=DF,由上知根据上...
(1) , ,DE,DE,DG,△CBH,△DEG. (2)证明见解析.
【解析】试题分析:(1)因为B是AC的中点, 同理因为AC=DF,由上知根据上面求得: 即可得△CBH≌△DEG.两个三角形对应的三边相等,则两个三角形全等,所以找出三角形对应的三边
(2)根据题中条件分析,再用SAS来证明即可
试题解析:(1)因为B是AC的中点, 同理
因为AC=DF,由上知根据上... 
