题目内容
一个直角三角形有两条边长为3，4，则较小的锐角约为（ ）
A. 37° B. 41° C. 37°或41° D. 以上答案均不对
C
【解析】试题解析：①若3、4是直角边，
∵两直角边为3，4，
∴斜边长==5，
∴较小的锐角所对的直角边为3，则其正弦值为；
②若斜边长为4，则较小边=≈2.65，
∴较小边所对锐角正弦值约==0.6625，
利用计算器求得角约为37°或41°．
故选C．
53随堂测系列答案在Rt△ABC中，∠C=90°，∠A、∠B、∠C所对的边分别为a、b、c，下列等式中不一定成立的是（ ）
A. b=atanB B. a=ccosB C. c＝
D. a=bcosA
D
【解析】∵∠C=90°，∠A、∠B、∠C所对的边分别为a、b、c，
∴A.tanB= ，则b=atanB，故本选项正确，
B.cosB= ，故本选项正确，
C.sinA= ，故本选项正确，
D.cosA= ，故本选项错误，
故选D． 小红到文具商店买彩笔，每打彩笔12支，售价18元，那么买彩笔所需的钱数y(元)与购买彩笔的支数x(支)之间的关系式为( )
A. y＝1.5x B. y＝x C. y＝12x D. y＝18x
A
【解析】根据钱数=单价×数量可得： .
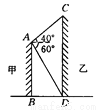
故选A. 如图所示，两建筑物的水平距离为24 m，从A点测得D点的俯角为60°，测得C点的仰角为40°，求这两座建筑物的高．(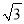
≈1.732，tan 40°≈0.8391，精确到0.01 m)
61.7l m
【解析】试题分析：过点A作AE⊥CD于点E，可得四边形ABDE为矩形，AB=ED，BD=AE，然后在Rt△AED和Rt△AEC中，分别求出DE和EC的长度，继而可求得建筑物CD的高度和建筑物AB的高度．
试题解析：作AE⊥CD于E，
则AE=BD=24m，
在Rt△AED中，tan∠DAE=，
∴DE=AEtan 60°≈24×1.732≈41.57(... 在△ABC中，∠C-90°，若tanB=2，a=1，则b=________．
2
【解析】试题解析：在Rt△ABC中，
∵∠C=90°，
∴AB为斜边．
∴b=AC•tanB
=a•tanB
=2．
故答案为：2. 在△ABC中，如果∠B＝65°，∠A的外角等于130°，那么△ABC___(填“是”或“不是”)等腰三角形．
是
【解析】在△ABC中，∠A的外角等于130°，可得∠A=50°，又因∠B=65°，根据三角形的内角和定理可得∠C=65°，所以∠B=∠C，即可得△ABC是等腰三角形． 如图所示为农村居民住宅侧面截面图，屋坡AF、AG分别架在墙体的点B，点C处，且AB＝AC，侧面四边形BDEC为长方形．若测得∠FAG＝110°，则∠FBD＝( )
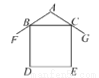
A. 35° B. 40° C. 55° D. 70°
C
【解析】在△ABC中，AB＝AC，∠BAC＝110°，根据等腰三角形的性质和三角形的内角和定理可得∠ABC=35°，由四边形BDEC为长方形可得∠DBC=90°，再由平角的定义可得∠FBD=180°-∠ABC-∠DBC=180°-35°-90°=55°，故选C. 国家规定，中小学生每天在校体育活动时间不低于1小时，为了解这项政策的落实情况，有关部门就“你某天在校体育活动时间是多少”的问题，在某校随机抽查了部分学生，再根据活动时间t（小时）进行分组（A组：t＜0.5，B组：0.5≤t＜1，C组：1≤t＜1.5，D组：t≥1.5），绘制成如下两幅不完整统计图，请根据图中信息回答问题：
（1）此次抽查的学生数为 人；
（2）补全条形统计图；
（3）从抽查的学生中随机询问一名学生，该生当天在校体育活动时间低于1小时的概率是 ；
（4）若当天在校学生数为1200人，请估计在当天达到国家规定体育活动时间的学生有 人．
（1）300；（2）补图见解析；（3）40%；（4）720人.
【解析】试题分析：（1）根据题意即可得到结论；
（2）求出C组的人数，A组的人数补全条形统计图即可；
（3）根据概率公式即可得到结论；
（4）用总人数乘以达到国家规定体育活动时间的百分比即可得到结论．
试题解析：（1）60÷20%=300（人），
答：此次抽查的学生数为300人.
故答案为：3... 如图，在△ABC中，∠BAC是钝角，画出：
(1)∠BAC的平分线；
(2)AC边上的中线；
(3)AC边上的高；
(4)AB边上的高．
作图见解析.
【解析】试题分析：（1）根据作已知角的角平分线的步骤作出图形；
（2）关键是找出线段AC的中点，要作出线段AC的垂直平分线，将所得中点与点B连结即可得到AC边上的中线；
（3）（4）根据过一点作已知直线垂线的方法，作出AC和AB边上的高，
试题解析：（1）∠BAC的平分线作法如下：
①以点A为圆心，定长为半径画弧，分别交AB、AC于D、E两点；
②...