题目内容
如图,点D,E在△ABC的边BC上,AB=AC,BD=CE.
求证:AD=AE.
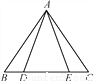
 证明见解析
【解析】试题分析:利用等腰三角形的性质得到∠B=∠C,然后证明△ABD≌△ACE即可证得结论.
【解答】证明:∵AB=AC,
∴∠B=∠C,
在△ABD与△ACE中,
∵,
∴△ABD≌△ACE(SAS),
∴AD=AE.
证明见解析
【解析】试题分析:利用等腰三角形的性质得到∠B=∠C,然后证明△ABD≌△ACE即可证得结论.
【解答】证明:∵AB=AC,
∴∠B=∠C,
在△ABD与△ACE中,
∵,
∴△ABD≌△ACE(SAS),
∴AD=AE.
练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
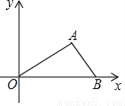
如图,在平面直角坐标系xOy中,已知点A(2,1)和点B(3,0),则sin∠AOB的值等于( )
A. 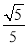 B.
B. 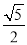 C.
C. 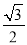 D.
D. 
 A
【解析】试题解析:过A作AC⊥x轴,
∵A(2,1),
∴AC=1,OC=2,
在Rt△AOC中,根据勾股定理得:OA=,
则sin∠AOB=,
故选A
A
【解析】试题解析:过A作AC⊥x轴,
∵A(2,1),
∴AC=1,OC=2,
在Rt△AOC中,根据勾股定理得:OA=,
则sin∠AOB=,
故选A 如图,∠1=∠2,P为BN上一点,且PD⊥BC于点D,AB+BC=2BD.试说明:∠BAP+∠BCP=180°.

 见解析
【解析】作PE垂直于AB于E,根据角平分线的性质可知PD=PE,HL定理可知△PBD≌△PBE,可得BD=BE,根据题中线段和差的关系,可得△PAE≌△PCD,所以可知∠PAE=∠PCD,根据∠PAE+∠PAB=180°,即可证明题中关系.
证明:如图,过点P作PE⊥BA于E.
∵PD⊥BC,PE⊥BM,∠1=∠2,
∴PD=PE.
∵PD⊥BC,PE⊥BM,...
见解析
【解析】作PE垂直于AB于E,根据角平分线的性质可知PD=PE,HL定理可知△PBD≌△PBE,可得BD=BE,根据题中线段和差的关系,可得△PAE≌△PCD,所以可知∠PAE=∠PCD,根据∠PAE+∠PAB=180°,即可证明题中关系.
证明:如图,过点P作PE⊥BA于E.
∵PD⊥BC,PE⊥BM,∠1=∠2,
∴PD=PE.
∵PD⊥BC,PE⊥BM,... 如图,学校的保管室里,有一架5米长的梯子斜靠在墙上,此时梯子与地面所成的角为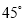 ,如果梯子的底端
,如果梯子的底端 固定不动,顶端靠在对面墙上,此时梯子与地面所成的角为
固定不动,顶端靠在对面墙上,此时梯子与地面所成的角为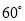 ,求此保管室的宽度
,求此保管室的宽度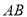 的长.
的长.
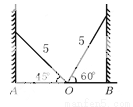
 【解析】由于两边的墙都和地面垂直,所以构成了两个直角三角形.
∵cos45°==,∴;而cos60°==,∴BO=.
∴AB=AO+BO==.
【解析】由于两边的墙都和地面垂直,所以构成了两个直角三角形.
∵cos45°==,∴;而cos60°==,∴BO=.
∴AB=AO+BO==. 如图,已知正方形ABCD的边长为2,如果将线段BD绕着点B旋转后,点D落在CB的延长线上的点 处,那么tan∠BAD′等于( )
处,那么tan∠BAD′等于( )
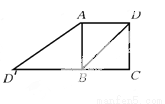
A. 1 B. 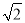 C.
C. 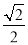 D.
D. 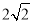
 B
【解析】试题解析:正方形ABCD的边长为2,则对角线BD=.
∴BD′=BD=.
∴tan∠BAD’=.
故选B.
B
【解析】试题解析:正方形ABCD的边长为2,则对角线BD=.
∴BD′=BD=.
∴tan∠BAD’=.
故选B. 如图,在△ABC中,AB=AC,∠ABC=75°,E为BC延长线上一点,∠ABC与∠ACE的平分线相交于点D,则∠D的度数为( )
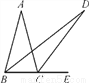
A. 15° B. 17.5° C. 20° D. 22.5°
 A
【解析】因为AB=AC,∠ABC=75°,所以∠A=30°.
因为∠ABC与∠ACE的平分线相交于点D,所以∠ABD=∠EBD,∠ACD=∠ECD.
设ABD=∠EBD=x,∠ACD=∠ECD=y,则
2y=2x+30°①,
y=x+∠D ②
联立①②得,∠D=15°.
故选A.
A
【解析】因为AB=AC,∠ABC=75°,所以∠A=30°.
因为∠ABC与∠ACE的平分线相交于点D,所以∠ABD=∠EBD,∠ACD=∠ECD.
设ABD=∠EBD=x,∠ACD=∠ECD=y,则
2y=2x+30°①,
y=x+∠D ②
联立①②得,∠D=15°.
故选A. 如图所示,F、C在线段BE上,且∠1=∠2,BC=EF.若要根据“SAS”使△ABC≌△DEF,还需要补充的条件是________.
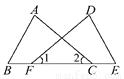
 AC=DF
【解析】已知∠1=∠2,BC=EF,根据“SAS”使△ABC≌△DEF,还需要补充的条件是AC=DF.
AC=DF
【解析】已知∠1=∠2,BC=EF,根据“SAS”使△ABC≌△DEF,还需要补充的条件是AC=DF. 甲.乙.丙三个事件发生的概率分别为0.5,0.1,0.9,它们各与下面的哪句话相配.
(1)发生的可能性很大,但不一定发生;
(2)发生的可能性很小;
(3)发生与不发生的可能性一样.
 (1)发生的概率为0.9.
(2)发生的概率为0.1.
(3)发生的概率为0.5.
【解析】试题分析:
(1)概率比较大;
(2)概率比较小;
(3)概率为0.5.
试题解析:
(1)发生的可能性很大,但不一定发生,匹配发生的概率为0.9.
(2)发生的可能性很小,匹配发生的概率为0.1.
(3)发生与不发生的可能性一样,匹配发生的概率为...
(1)发生的概率为0.9.
(2)发生的概率为0.1.
(3)发生的概率为0.5.
【解析】试题分析:
(1)概率比较大;
(2)概率比较小;
(3)概率为0.5.
试题解析:
(1)发生的可能性很大,但不一定发生,匹配发生的概率为0.9.
(2)发生的可能性很小,匹配发生的概率为0.1.
(3)发生与不发生的可能性一样,匹配发生的概率为... 如图,A、B、C分别是线段A1B、B1C、C1A的中点,若△ABC的面积是1,那么△A1B1C1的面积为____.

 7
【解析】试题分析:如下图,连接A1C,B1A,C1B,,因B是线段B1C的中点,所以B1B="BC." △A1B1A和△AB1B等底同高,根据等底同高的两个三角形面积相等可得S△B1AB=S△ABC=1;同理可得S△A1B1A=S△AB1B=1;所以=S△A1B1A+S△AB1B=1+1=2;同理可得S△C1CB1=2, S△C1AA1=2.
S△A1B1C1= S△A1BB1+ ...
7
【解析】试题分析:如下图,连接A1C,B1A,C1B,,因B是线段B1C的中点,所以B1B="BC." △A1B1A和△AB1B等底同高,根据等底同高的两个三角形面积相等可得S△B1AB=S△ABC=1;同理可得S△A1B1A=S△AB1B=1;所以=S△A1B1A+S△AB1B=1+1=2;同理可得S△C1CB1=2, S△C1AA1=2.
S△A1B1C1= S△A1BB1+ ... 
