各边长均为整数且三边各不相等的三角形的周长小于13，这样的三角形个数共有( )
A. 5个 B. 4个 C. 3个 D. 2个
C
【解析】试题解析：根据三角形的两边之和大于第三边以及三角形的周长小于13，则其中的任何一边不能超过6.5；
再根据两边之差小于第三边，则这样的三角形共有3，4，2；4，5，2；3，4，5三个.
故选C. 五条线段的长分别为1，2，3，4，5，以其中任意三条线段为边长可以________个三角形．
3
【解析】试题解析：由三角形的两边之和大于第三边,两边之差小于第三边可知
在所给数组中能组成三角形的是2、3、4;2、4、5和3、4、5三组.
故答案为：3. 一个三角形的三个内角的度数的比是2：2：1，这个三角形是_________三角形．
锐角（等腰锐角）
【解析】试题解析：一个三角形的三个内角的度数的比是2:2:1，则一定有两个角相等，则三角形是：等腰三角形，
底角一定大于顶角，则三角形一定是锐角三角形.
故答案是：锐角(等腰锐角). 一个等腰三角形两边的长分别是15cm和7cm则它的周长是__________．
37cm
【解析】①7cm是腰长时，三角形的三边分别为7cm、7cm、15cm，
∵7+7=14<15，
∴不能组成三角形，
②7cm是底边时，三角形的三边分别为7cm、15cm、15cm，
能组成三角形，
周长=7+15+15=37cm，
综上所述，它的周长是37cm.
故答案为：37cm. 直角三角形中，两个锐角的差为40°，则这两个锐角的度数分别为_________．
65°和25°
【解析】试题解析：设这两个锐角的度数分别为x，y，
根据题意得,
解得
故答案为： 在△ABC中，∠A－∠B=30°、∠C=4∠B，则∠C=________．
100°
【解析】试题解析：
①，
②，
①?②得, 解得
故答案为： 如图5—13，在△ABC中，AD⊥BC，GC⊥BC，CF⊥AB，BE⊥AC，垂足分别为D、C、F、E，则_______是△ABC中BC边上的高，_________是△ABC中AB边上的高，_________是 △ABC中AC边上的高，CF是△ABC的高，也是△_______、△_______、△_______、△_________的高．
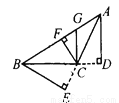
AD CF BE BFC FGC FAC GAC
【解析】试题解析：AD是△ABC中BC边上的高，是△ABC中AB边上的高，BE是△ABC中AC边上的高，CF是△ABC的高，也是△BFC、△FGC、△FAC、△GAC的高.
故答案是：AD、CF、BE、BFC、FGC、FAC、GAC. 如图，△ABC的两个外角的平分线相交于点D，如果∠A=50°，那么∠D=_____．
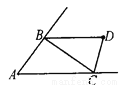
65°
【解析】试题解析：
故答案为：