题目内容
一个三角形的三个内角的度数的比是2：2：1，这个三角形是_________三角形．
锐角（等腰锐角）
【解析】试题解析：一个三角形的三个内角的度数的比是2:2:1，则一定有两个角相等，则三角形是：等腰三角形，
底角一定大于顶角，则三角形一定是锐角三角形.
故答案是：锐角(等腰锐角).
练习册系列答案
阅读快车系列答案
相关题目
如果两个角不相等，那么这两个角不是对顶角。 （___）
√
【解析】试题分析：对顶角的两个角的度数肯定相等；度数相等的角不一定是对顶角．故本题的答案为“√”． 已知点P(a，3)和P’(-4，b)关于原点对称，则(a+b)的值为__________.
1
【解析】因为点P(a,3)和P’(-4,b)关于原点对称,所以a+(－4)=0,3+b=0,所以a=4，b=－3,所以a+b=4+(－3)=1,故答案为:1. 一个飞机零件的形状如图5—19所示，按规定∠A应等于90°，∠B，∠D应分别是20°和30°，康师傅量得∠BCD=143°，就能断定这个零件不合格，你能说出其中的道理吗?
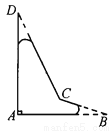
不合格，理由见解析.
【解析】试题分析：延长BC与AD相交于点E，根据三角形的一个外角等于与它不相邻的两个内角的和求出∠BCD即可判断．
试题解析：如图，延长BC与AD相交于点E，
∵∠1是△ABE的外角,
同理,
∵李师傅量得不是
∴这个零件不合格. 如图5—13，在△ABC中，AD⊥BC，GC⊥BC，CF⊥AB，BE⊥AC，垂足分别为D、C、F、E，则_______是△ABC中BC边上的高，_________是△ABC中AB边上的高，_________是 △ABC中AC边上的高，CF是△ABC的高，也是△_______、△_______、△_______、△_________的高．
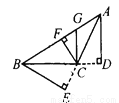
AD CF BE BFC FGC FAC GAC
【解析】试题解析：AD是△ABC中BC边上的高，是△ABC中AB边上的高，BE是△ABC中AC边上的高，CF是△ABC的高，也是△BFC、△FGC、△FAC、△GAC的高.
故答案是：AD、CF、BE、BFC、FGC、FAC、GAC. 已知：a、b、c是△ABC三边长，且M=(a＋b＋c)(a＋b－c)(a－b－c)，那么 ( )
A. M＞0 B. M=0 C. M＜0 D. 不能确定
C
【解析】试题解析：∵a、b、c是△ABC三边长，
∴a+b+c>0，a+b?c>0，a?b?c<0，
∴M=(a+b+c)(a+b?c)(a?b?c)<0.
故选C. 一个三角形的两边长为2和6，第三边为偶数．则这个三角形的周长为 ( )
A. 10 B. 12 C. 14 D. 16
C
【解析】试题解析：根据三角形的三边关系，得
6-2＜x＜6+2，
即4＜x＜8．
又∵第三边长是偶数，则x=6．
∴三角形的周长是2+6+6=14；
则该三角形的周长是14．
故选C. 下列图形是轴对称图形的是( )
A. 
B. 
C. 
D. 
A
【解析】根据轴对称图形的定义：如果一个图形沿着一条直线对折后两部分完全重合，这样的图形叫做轴对称图形，这条直线叫做对称轴；据此判断即可．.
【解析】
由轴对称图形的意义可知选项A中的图形是轴对称图形；而选项B、C、D中的图形均不是轴对称图形.
故选A. 如图，梯子（长度不变）跟地面所成的锐角为A，关于∠A的三角函数值与梯子的倾斜程度之间，叙述正确的是（ ）
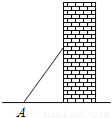
A. sinA的值越大，梯子越陡
B. cosA的值越大，梯子越陡
C. tanA的值越小，梯子越陡
D. 陡缓程度与∠A的函数值无关
A
【解析】试题分析：锐角三角函数值的变化规律：正弦值和正切值都是随着角的增大而增大，余弦值和余切值都是随着角的增大而减小．
【解析】
根据锐角三角函数的变化规律，知sinA的值越大，∠A越大，梯子越陡．
故选：A．