题目内容
五条线段的长分别为1，2，3，4，5，以其中任意三条线段为边长可以________个三角形．
3
【解析】试题解析：由三角形的两边之和大于第三边,两边之差小于第三边可知
在所给数组中能组成三角形的是2、3、4;2、4、5和3、4、5三组.
故答案为：3.
练习册系列答案
相关题目
如图表示的是汽车在行驶的过程中，速度随时间变化而变化的情况．
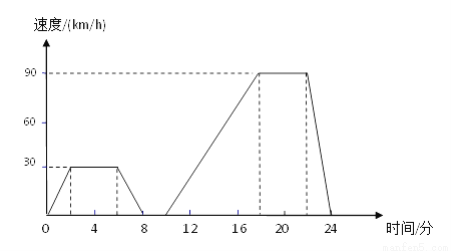
（1）汽车从出发到最后停止共经过了多少时间？它的最高时速是多少？
（2）汽车在那些时间段保持匀速行驶？时速分别是多少？
（3）出发后8分到10分之间可能发生了什么情况？
（4）用自己的语言大致描述这辆汽车的行驶情况．
（1）见解析；（2）见解析；（3）见解析；（4）见解析；
【解析】（1）汽车从出发到最后停止共经过了24min，它的最高时速是90km/h
（2）汽车大约在2分到6分，18分到22分之间保持匀速行驶，时速分别是30km/h 和90km/h
（3）出发后8分到10分速度为0，所以汽车是处于静止的。可能遇到了红灯或者障碍（或者遇到了朋友或者休息）。（答案不唯一，只要所说的情况合理即可... 点M(2，-3）与点N（2，3）关于______对称；点A(-2，-4）与点B（2，4）关于______对称；点G(4，0）与点H（-4，0）关于____________对称.
x轴 原点 y轴
【解析】根据关于x轴对称的点的坐标规律:横坐标相同,纵坐标互为相反数,关于原点的对称点,横纵坐标都变成相反数,关于y轴对称的点的坐标规律:横坐标互为相反数,纵坐标相同,
所以点M与点N关于x轴对称,点A与点B关于原点对称,点G与点H关于y轴对称,故答案为: x轴, 原点, y轴. 如图，点B、C、D、E共线，试问图中A、B、C、D、E五点可确定多少个三角形?说明理由．
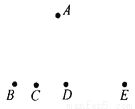
6个.
【解析】试题分析：经过两点可以确定一条线段，而不在同一条直线上的三条线段首尾顺次相接可组成一个三角形，因而三角形的个数就是B、C、D、E四点中，两个分成一组，点的组数．
试题解析：可以确定6个三角形.
理由：经过两点可以确定一条线段，而不在同一条直线上的三条线段首尾顺次相接可组成一个三角形，
所以图中可以确定6个三角形. 直角三角形中，两个锐角的差为40°，则这两个锐角的度数分别为_________．
65°和25°
【解析】试题解析：设这两个锐角的度数分别为x，y，
根据题意得,
解得
故答案为： 如图，已知∠ACB=90°，CD⊥AB，垂足是D，则图中与∠A相等的角是 ( )
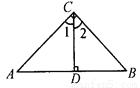
A. ∠1 B. ∠2 C. ∠B D. ∠1、∠2和∠B
B
【解析】试题解析：
∵∠ACB=即∠1+∠2=
又∵中,∠A+∠1=
∴∠A=∠2.
故选B. 已知a＝b＋2 018，求代数式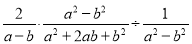
的值．
4036
【解析】试题分析：根据分式的乘除法，先对分子分母分解因式，然后把除法化为乘法，再约分，然后代入求值.
试题解析：原式＝××(a－b)(a＋b)＝2(a－b)．
∵a＝b＋2 018，∴原式＝2×2 018＝4 036. 将一个正方形按下列要求割成4块:
(1)分割后的整个图形必须是轴对称图形;
(2)所分得的4块图形是全等图形.
请你按照上述两个要求,分别在图①,②,③中的正方形中画出3种不同的分割方法.(不写画法)
答案不唯一,
【解析】分割后的整个图形必须是轴对称图形，作两边的中垂线；四块图形的完全相同，作法较多，符合要求即可．
【解析】
如图所示. 如果∠A为锐角，且sinA＝0.6，那么（ ）
A. 0°＜A＜30° B. 30°＜A＜45°
C. 45°＜A＜60° D. 60°＜A＜90°
B
【解析】∵sin30°="1/2," sin45°=,<0.6<
∴30°＜∠A＜45°，故选B