如图，∠1＝∠B，且∠2＝∠C，则下列结论不成立的是（ ）
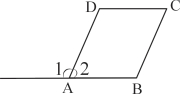
A、AD∥BC B、∠B＝∠C C、∠2＋∠B＝180° D、AB∥CD
B
【解析】
试题分析：由∠1＝∠B可得AD∥BC，再结合∠2＝∠C可得AB∥CD，再依次分析各选项即可作出判断.
∵∠1＝∠B
∴AD∥BC
∴∠2+∠B＝180°
∵∠2＝∠C
∴∠B+∠C＝180°
∴AB∥CD
故选B. 如图，直线AB、CD相交于点O，EF⊥AB于O，且∠COE=50°，则∠BOD等于（ ）
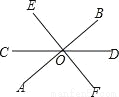
A. 40° B. 45° C. 55° D. 65°
A
【解析】∵EF⊥AB于O，∠COE=50°，
∴∠AOC=90°-50°=40°，
∵∠AOC与∠BOD是对顶角，
∴∠BOD=∠AOC=40°；
故选A。 如图，若AB∥CD，则∠A、∠E、∠D之间的关系是( )
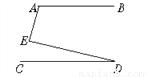
A. ∠A+∠E+∠D=180° B. ∠A－∠E+∠D=180°
C. ∠A+∠E－∠D=180° D. ∠A+∠E+∠D=270°
C
【解析】过点E作EF∥CD，
∵AB∥CD，
∴AB∥EF∥CD，
∴∠AEF=180°-∠A,∠DEF=∠D，
∴∠AED=∠AEF+∠DEF=180°-∠A+∠D；
即∠AED+∠A-∠D =180°.
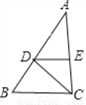
故选C. 如图，CD平分∠ACB，DE∥BC，∠AED=80°，求∠EDC的度数．
40°
【解析】试题分析：根据平行线的性质求出∠ACB的度数，根据角平分线定义求出即可.
试题解析：
∵ DE∥BC，∠AED =80°，∴ ∠EDC =∠BCD，∠ACB=∠AED=80°
∵ CD平分∠ACB，
∴ ∠BCD= ∠ACB=40°，∴ ∠EDC=∠BCD=40° 如图，已知AB∥CD，∠B=65°，CM平分∠BCE，∠MCN=90°，求∠DCN的度数．
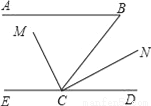
32.5°．
【解析】试题分析：已知AB∥CD，∠B=65°，根据平行线的性质可求得∠BCE =115°；再由角平分线的定义求得∠ECM的度数，即可求得∠DCN的度数．
试题解析：
∵ AB∥CD，∴ ∠B+∠BCE =180°（两直线平行，同旁内角互补）
∵ ∠B =65°，∴ ∠BCE =115°
∵ CM平分∠BCE，∴ ∠ECM=∠BCE =57.5°
... ∠1=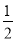
∠2，∠1+∠2=162°，求∠3与∠4的度数．
∠3=54°，∠4=72°
【解析】试题分析：先由∠1=∠2，∠1+∠2=162°，求出∠1和∠2的度数；再根据∠1和∠3 是对顶角，∠4和∠2为邻补角求出∠3与∠4的度数.
∵∠1=∠2，∠1+∠2=162°，
∴∠1=54°， ∠2=108°.
∵∠1和∠3是对顶角，
∴∠3=∠1=54°
∵∠2和∠4是邻补角，
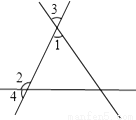
∴∠4=180°-∠2=180°-10... 如图，CD∥AB，∠DCB=70°，∠CBF=20°，∠EFB=130°，问直线EF与AB有怎样的位置关系，为什么？
平行
【解析】试题分析：由CD∥AB，∠DCB=70°可求出∠ABC==70°，进而求出∠ABF=50°，从而可得∠ABF+∠EFB=180°，根据同旁内角互补两直线平行可证EF∥AB.
证明:∵CD∥AB，
∴∠ABC=∠DCB=70°，
∠ABF=∠ABC-∠CBF=70°-20°=50°
∵∠ABF+∠EFB=50°+130°=180°
∴EF∥... 如图，AB∥CD，HP平分∠DHF，若∠AGH=80°，求∠DHP的度数.
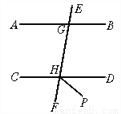
50°
【解析】试题分析：已知AB∥CD，联系平行线的性质不难得到∠EHD的大小，那么∠FHD的大小也就出来了；观察图形，利用角平分线的性质，即可得到∠DHP的大小.
【解析】
∵AB∥CD，
∴∠CHF=∠AGH=80°，
∴∠DHF=180°-80°=100°.
又∵HP平分∠DHF，
∴∠DHP=∠DHF=50°. 根据下列证明过程填空：
如图，已知BD⊥AC，EF⊥AC，D、F分别为垂足，且∠1=∠4，求证：∠ADG=∠C
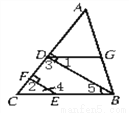
证明：∵BD⊥AC，EF⊥AC
∴∠2=∠3=90°（ ）
∴BD∥EF ( )
∴∠4=_____( )
∵∠1=∠4
∴∠1=_____( )
∴DG∥BC( )
∴∠ADG=∠C( )
见解析
【解析】试题分析：解决问题要熟悉平行线的性质和判定，能正确运用语言叙述理由，还要注意平行线的性质和判定的综合运用．
试题解析：∵BD⊥AC，EF⊥AC（已知），
∴∠2=∠3=90°，
∴BD∥EF（同位角相等，两直线平行），
∴∠4=∠5（两直线平行，同位角相等）；
∵∠1=∠4（已知），
∴∠1=∠5（等量代换），
∴DG∥BC（内错角相... 阅读下面的证明过程，指出其错误.
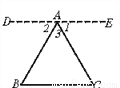
已知△ABC
求证：∠A+∠B+∠C=180°
证明：过A作DE∥BC，且使∠1=∠C
∵DE∥BC(画图)
∴∠2=∠B(两直线平行，内错角相等)
∵∠1=∠C(画图)
∴∠B+∠C+∠3=∠2+∠1+∠3=180°
即∠BAC+∠B+∠C=180°
答案见解析
【解析】试题分析：注意作辅助线的方法，过点A作的辅助线不能同时满足两个条件．只能作平行线后，根据平行线的性质得到∠1=∠C．
错误①：过A作DE∥BC，且使∠1=∠C，应改为：过A作DE∥BC.
错误②：∵∠1=∠C(画图)，理由错，应改为：两直线平行，内错角相等.