��Ŀ����
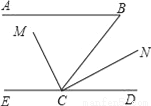
��ͼ����֪AB��CD����B=65�㣬CMƽ�֡�BCE����MCN=90�㣬���DCN�Ķ�����
 32.5�㣮
�������������������֪AB��CD����B=65�㣬����ƽ���ߵ����ʿ���á�BCE =115�㣻���ɽ�ƽ���ߵĶ�����á�ECM�Ķ�����������á�DCN�Ķ�����
���������
�� AB��CD���� ��B+��BCE =180�㣨��ֱ��ƽ�У�ͬ���ڽǻ�����
�� ��B =65�㣬�� ��BCE =115��
�� CMƽ�֡�BCE���� ��ECM=��BCE =57.5��
...
32.5�㣮
�������������������֪AB��CD����B=65�㣬����ƽ���ߵ����ʿ���á�BCE =115�㣻���ɽ�ƽ���ߵĶ�����á�ECM�Ķ�����������á�DCN�Ķ�����
���������
�� AB��CD���� ��B+��BCE =180�㣨��ֱ��ƽ�У�ͬ���ڽǻ�����
�� ��B =65�㣬�� ��BCE =115��
�� CMƽ�֡�BCE���� ��ECM=��BCE =57.5��
...
���������У����ж���ABCΪֱ�������ε���( )
A. ��A=��B=��C B. ��A����B=2��C
C. ��A�á�B�á�C=1��2��3 D. ��A=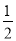 ��B=
��B=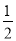 ��C
��C
 C
�����������������A. ����A=��B=��C����ȷ����ABCΪֱ�������Σ�����Aѡ�����
B�� ,����A+��B=2��C,������Bѡ�����
C. ,����A�á�B�á�C=1��2��3,������Cѡ����ȷ��
D. ����������Dѡ�����.
��ѡC.
C
�����������������A. ����A=��B=��C����ȷ����ABCΪֱ�������Σ�����Aѡ�����
B�� ,����A+��B=2��C,������Bѡ�����
C. ,����A�á�B�á�C=1��2��3,������Cѡ����ȷ��
D. ����������Dѡ�����.
��ѡC. ֱ��������ֽƬ����ֱ�DZ߳��ֱ�Ϊ6��8���ֽ���ABC��ͼ�����۵���ʹ��A���B�غϣ��ۺ�ΪDE����tan��CBE��ֵ�ǣ� ��
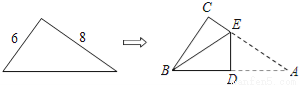
A. 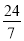 B.
B. 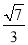 C.
C. 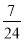 D.
D. 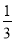
 C
����������������������۵��任�����ʿ�֪AE=BE����CE=x����֪BE=8-x�����ݹ��ɶ����ã��������x=����˿���tan��CBE=��
��ѡC
C
����������������������۵��任�����ʿ�֪AE=BE����CE=x����֪BE=8-x�����ݹ��ɶ����ã��������x=����˿���tan��CBE=��
��ѡC ��Rt��ABC�У���C��90�㣬����˵����ȷ����( )
��sinA��cosA����sin2A��cos2A��1����tanA��tanB��1����tanA��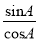
A. �٢ڢ� B. �ڢۢ� C. �٢ۢ� D. �٢ڢۢ�
 B
���������ߡ�C=90�㣬�࣬��֪�в�֪BC��AC�ڴ�С��ϵ���ʢٴ���
���ʢ���ȷ��
���ʢ���ȷ��
���ʢ���ȷ��
��ѡB.
B
���������ߡ�C=90�㣬�࣬��֪�в�֪BC��AC�ڴ�С��ϵ���ʢٴ���
���ʢ���ȷ��
���ʢ���ȷ��
���ʢ���ȷ��
��ѡB. �Ķ������֤�����̣�ָ�������.
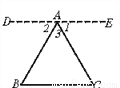
��֪��ABC
��֤����A+��B+��C=180��
֤������A��DE��BC����ʹ��1=��C
��DE��BC(��ͼ)
���2=��B(��ֱ��ƽ�У��ڴ������)
�ߡ�1=��C(��ͼ)
���B+��C+��3=��2+��1+��3=180��
����BAC+��B+��C=180��
 �𰸼�����
�����������������ע���������ߵķ���������A���ĸ����߲���ͬʱ��������������ֻ����ƽ���ߺ���ƽ���ߵ����ʵõ���1=��C��
����٣���A��DE��BC����ʹ��1=��C��Ӧ��Ϊ����A��DE��BC.
����ڣ��ߡ�1=��C(��ͼ)�����ɴ���Ӧ��Ϊ����ֱ��ƽ�У��ڴ������.
�𰸼�����
�����������������ע���������ߵķ���������A���ĸ����߲���ͬʱ��������������ֻ����ƽ���ߺ���ƽ���ߵ����ʵõ���1=��C��
����٣���A��DE��BC����ʹ��1=��C��Ӧ��Ϊ����A��DE��BC.
����ڣ��ߡ�1=��C(��ͼ)�����ɴ���Ӧ��Ϊ����ֱ��ƽ�У��ڴ������. �����1���2��������1���3���࣬��ô ( )
A. ��2����3 B. ��2=��3 C. ��2����3 D. ��2�ݡ�3
 A
���������ߡ�1���2���������1+��2=180�㣬
�ߡ�1���3���࣬���1+��3=90�㣬
���1+��2-����1+��3��=180��-90�㣬
���2-��3=90�㣬
���2����3��
��ѡA��
A
���������ߡ�1���2���������1+��2=180�㣬
�ߡ�1���3���࣬���1+��3=90�㣬
���1+��2-����1+��3��=180��-90�㣬
���2-��3=90�㣬
���2����3��
��ѡA�� ��ͼ,DAE��һ��ֱ��,DE��BC�����BAC=___��.
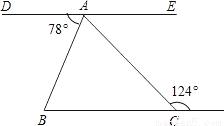
 46�㣮
�������������������DE��BC�����DAC=124�㣬���BAC=��DAC����DAB=124�㩁78��=46�㣮�ʴ�Ϊ��46�㣮
46�㣮
�������������������DE��BC�����DAC=124�㣬���BAC=��DAC����DAB=124�㩁78��=46�㣮�ʴ�Ϊ��46�㣮 ��֪��ABC����ֱ��MN�Գƣ�������˵��������ǣ�������
A. ��ABC�б���һ��������ֱ��MN��
B. ��ABC������������
C. ��ABC���������������
D. ��ABC�б�����һ���ǵ���60��
 D
����������������
�ߡ�ABC����ֱ��MN�Գƣ����ABCΪ���������Σ���Գ���Ϊ�ױ��ϵĸ����ڵ�ֱ�ߣ�
A����ABC�б���һ��������ֱ��MN�ϣ��ʱ�ѡ����ȷ��
B����ABC�б�����������ȣ��ʱ�ѡ����ȷ��
C����ABC�У�������������ȣ��ʱ�ѡ����ȷ��
D�����õ����������ǵȱ�������ʱ����ABC����һ���ǵ���60�㣬�ʱ�ѡ�����
��ѡD��
D
����������������
�ߡ�ABC����ֱ��MN�Գƣ����ABCΪ���������Σ���Գ���Ϊ�ױ��ϵĸ����ڵ�ֱ�ߣ�
A����ABC�б���һ��������ֱ��MN�ϣ��ʱ�ѡ����ȷ��
B����ABC�б�����������ȣ��ʱ�ѡ����ȷ��
C����ABC�У�������������ȣ��ʱ�ѡ����ȷ��
D�����õ����������ǵȱ�������ʱ����ABC����һ���ǵ���60�㣬�ʱ�ѡ�����
��ѡD�� ����ͼ���У�������Գ�ͼ�ε���(����)
A. ���ഹֱ������ֱ�߹��ɵ�ͼ�� B. һ��ֱ�ߺ�ֱ����һ�㹹�ɵ�ͼ��
C. ��һ���ڽ�Ϊ30�㣬��һ���ڽ�Ϊ120��������� D. ��һ���ڽ�Ϊ60���������
 D
����������������
ѡ��A����4���Գ��B����һ���Գ��C��һ���Գ��ᣮ��ѡD��
D
����������������
ѡ��A����4���Գ��B����һ���Գ��C��һ���Գ��ᣮ��ѡD�� 
