题目内容
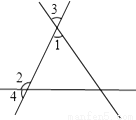
∠1=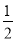 ∠2,∠1+∠2=162°,求∠3与∠4的度数.
∠2,∠1+∠2=162°,求∠3与∠4的度数.
 ∠3=54°,∠4=72°
【解析】试题分析:先由∠1=∠2,∠1+∠2=162°,求出∠1和∠2的度数;再根据∠1和∠3 是对顶角,∠4和∠2为邻补角求出∠3与∠4的度数.
∵∠1=∠2,∠1+∠2=162°,
∴∠1=54°, ∠2=108°.
∵∠1和∠3是对顶角,
∴∠3=∠1=54°
∵∠2和∠4是邻补角,
∴∠4=180°-∠2=180°-10...
∠3=54°,∠4=72°
【解析】试题分析:先由∠1=∠2,∠1+∠2=162°,求出∠1和∠2的度数;再根据∠1和∠3 是对顶角,∠4和∠2为邻补角求出∠3与∠4的度数.
∵∠1=∠2,∠1+∠2=162°,
∴∠1=54°, ∠2=108°.
∵∠1和∠3是对顶角,
∴∠3=∠1=54°
∵∠2和∠4是邻补角,
∴∠4=180°-∠2=180°-10...
练习册系列答案
相关题目
如图,在四边形ABCD中,AB=AD,CB=CD,若连接AC、BD相交于点O,则图中全等三角形共有( )
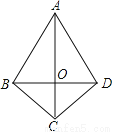
A. 1对 B. 2对 C. 3对 D. 4对
 C
【解析】试题分析:在△ABC和△ADC中,根据全等三角形的判定SSS可得△ABC≌△ADC(SSS),根据全等三角形的性质可得∠BAC=∠DAC,∠BCA=∠DCA,在△ABO和△ADO中,可得△ABO≌△ADO(SAS),然后在△BOC和△DOC中,可得△BOC≌△DOC(SAS),
故选:C.
C
【解析】试题分析:在△ABC和△ADC中,根据全等三角形的判定SSS可得△ABC≌△ADC(SSS),根据全等三角形的性质可得∠BAC=∠DAC,∠BCA=∠DCA,在△ABO和△ADO中,可得△ABO≌△ADO(SAS),然后在△BOC和△DOC中,可得△BOC≌△DOC(SAS),
故选:C. 如图,已知直线l1∥l2∥l3∥l4,相邻两条平行直线间的距离都是1.如果正方形ABCD的四个顶点分别在四条直线上,那么sinα=_.
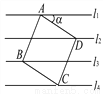
 【解析】过D作EF⊥l1,交l1于E,交l4于F,
∵EF⊥l1,l1∥l2∥l3∥l4,
∴EF和l2,l3,l4的夹角都是90°,
即EF与l2,l3,l4都垂直,
∴DE=1,DF=2.
∵四边形ABCD是正方形,
∴∠ADC=90°,AD=CD,
∴∠ADE+∠CDF=90°,
又∵∠α+∠ADE=90°,
∴∠α=∠CDF,
∵...
【解析】过D作EF⊥l1,交l1于E,交l4于F,
∵EF⊥l1,l1∥l2∥l3∥l4,
∴EF和l2,l3,l4的夹角都是90°,
即EF与l2,l3,l4都垂直,
∴DE=1,DF=2.
∵四边形ABCD是正方形,
∴∠ADC=90°,AD=CD,
∴∠ADE+∠CDF=90°,
又∵∠α+∠ADE=90°,
∴∠α=∠CDF,
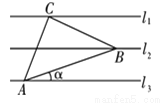
∵... 如图,已知l1∥l2∥l3,相邻两条平行直线间的距离相等,若等腰直角△ABC的三个顶点分别在这三条平行直线上,则sina的值是( )
A. 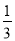 B.
B. 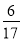 C.
C. 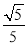 D.
D. 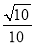
 D
【解析】如图,分别过点A,B作AE⊥l1,BF⊥l1,垂足分别为E,F,BF与l3交于点D,
则易由AAS证明△AEC≌△CFB。
设平行线间距离为d=1,
则CE=BF=1,AE=CF=2,AC=BC=,AB=。
∴。故选D。
D
【解析】如图,分别过点A,B作AE⊥l1,BF⊥l1,垂足分别为E,F,BF与l3交于点D,
则易由AAS证明△AEC≌△CFB。
设平行线间距离为d=1,
则CE=BF=1,AE=CF=2,AC=BC=,AB=。
∴。故选D。 已知:如图,CB⊥AB,CE平分∠BCD,DE平分∠CDA,∠1+∠2=90°,求证:DA⊥AB.
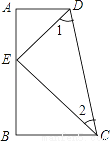
 证明见解析.
【解析】试题分析:根据CE平分∠BCD,DE平分∠CDA,得出∠1+∠2=(∠ADC+∠BCD)=90°,∠ADC+∠BCD=180°,证出AD∥BC,再根据CB⊥AB,即可得出DA⊥AB.
【解析】
∵CE平分∠BCD,DE平分∠CDA,
∴∠1=∠ADC,∠2=∠BCD,
∴∠1+∠2=∠ADC+∠BCD=(∠ADC+∠BCD)=90°,
∴∠AD...
证明见解析.
【解析】试题分析:根据CE平分∠BCD,DE平分∠CDA,得出∠1+∠2=(∠ADC+∠BCD)=90°,∠ADC+∠BCD=180°,证出AD∥BC,再根据CB⊥AB,即可得出DA⊥AB.
【解析】
∵CE平分∠BCD,DE平分∠CDA,
∴∠1=∠ADC,∠2=∠BCD,
∴∠1+∠2=∠ADC+∠BCD=(∠ADC+∠BCD)=90°,
∴∠AD... 如图,∠1=∠B,且∠2=∠C,则下列结论不成立的是( )
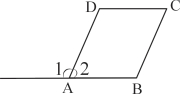
A、AD∥BC B、∠B=∠C C、∠2+∠B=180° D、AB∥CD
 B
【解析】
试题分析:由∠1=∠B可得AD∥BC,再结合∠2=∠C可得AB∥CD,再依次分析各选项即可作出判断.
∵∠1=∠B
∴AD∥BC
∴∠2+∠B=180°
∵∠2=∠C
∴∠B+∠C=180°
∴AB∥CD
故选B.
B
【解析】
试题分析:由∠1=∠B可得AD∥BC,再结合∠2=∠C可得AB∥CD,再依次分析各选项即可作出判断.
∵∠1=∠B
∴AD∥BC
∴∠2+∠B=180°
∵∠2=∠C
∴∠B+∠C=180°
∴AB∥CD
故选B. 如图,AB∥CD,AD∥BC,则图中与∠A相等的角有_____个.
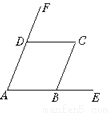
 3
【解析】∵AB∥CD,
∴∠A=∠CDF, ∠CBE=∠C;
∵AD∥BC,
∴∠A=∠CBE,
∴∠A=∠CDF=∠CBE=∠C.
∴与∠A相等的角有3个.
3
【解析】∵AB∥CD,
∴∠A=∠CDF, ∠CBE=∠C;
∵AD∥BC,
∴∠A=∠CBE,
∴∠A=∠CDF=∠CBE=∠C.
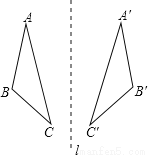
∴与∠A相等的角有3个. 如图,△ABC和△A′B′C′关于直线l对称,求证:△ABC≌△A′B′C′.若△ABC≌△A′B′C′,那么△ABC和△A′B′C′一定关于某条直线l对称吗?若一定请给出证明,若不一定请画出反例图。
 见解析
【解析】试题分析:根据轴对称的定义即可证明;举反例可以说明全等不一定轴对称.
试题解析:【解析】
∵△ABC和△A′B′C′关于直线l对称,∴△ABC和△A′B′C′能够完全重合,∴△ABC≌△A′B′C′.
若△ABC≌△A′B′C′,△ABC和△A′B′C′不一定一定关于某条直线l对称,如图所示.
见解析
【解析】试题分析:根据轴对称的定义即可证明;举反例可以说明全等不一定轴对称.
试题解析:【解析】
∵△ABC和△A′B′C′关于直线l对称,∴△ABC和△A′B′C′能够完全重合,∴△ABC≌△A′B′C′.
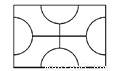
若△ABC≌△A′B′C′,△ABC和△A′B′C′不一定一定关于某条直线l对称,如图所示. 我国传统的木房屋窗子常用各种图案装饰,如图是一种常见图案,这个图案有____条对称轴.
 2
【解析】试题分析:根据轴对称图形的概念:如果一个图形沿一条直线折叠后,直线两旁的部分能够互相重合,那么这个图形叫做轴对称图形.
这是一个组合图形,它的外部是一个长方形,再根据它的组合特点,显然有2条对称轴,即两组对边的垂直平分线.
故答案为2.
2
【解析】试题分析:根据轴对称图形的概念:如果一个图形沿一条直线折叠后,直线两旁的部分能够互相重合,那么这个图形叫做轴对称图形.
这是一个组合图形,它的外部是一个长方形,再根据它的组合特点,显然有2条对称轴,即两组对边的垂直平分线.
故答案为2. 
