题目内容
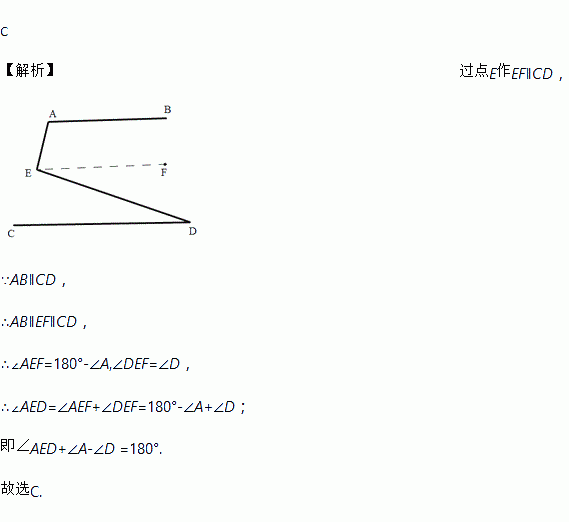
如图，若AB∥CD，则∠A、∠E、∠D之间的关系是( )
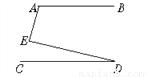
A. ∠A+∠E+∠D=180° B. ∠A－∠E+∠D=180°
C. ∠A+∠E－∠D=180° D. ∠A+∠E+∠D=270°
C
【解析】过点E作EF∥CD，
∵AB∥CD，
∴AB∥EF∥CD，
∴∠AEF=180°-∠A,∠DEF=∠D，
∴∠AED=∠AEF+∠DEF=180°-∠A+∠D；
即∠AED+∠A-∠D =180°.
故选C.
练习册系列答案
金状元绩优好卷系列答案
相关题目
如图，线段AD把△ABC分为面积相等的两部分，则线段AD是（ ）．
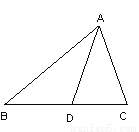
A. 三角形的角平分线 B. 三角形的中线
C. 三角形的高 D. 以上都不对
B
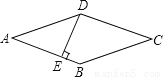
【解析】试题分析：三角形的中线将三角形的面积分成相等的两部分，角平分线是指将角分成度数相等的两个角. 如图，菱形ABCD的周长为20cm，DE⊥AB，垂足为E，cosA=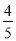
，则下列结论中正确的个数为（ ）
①DE=3cm；②EB=1cm；③S菱形ABCD=15cm2
．
A．3个 B．2个 C．1个 D．0个
A．
【解析】
试题解析：由题意可得，菱形的边长为5cm，又cosA=，所以AE=4，
则DE=3cm；EB=1cm；S菱形ABCD=5×3=15cm2，
故选A． 在△ABC中，若|sinA－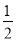
|＋(
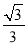－tanB)2＝0，则∠C的度数为( )
A. 30° B. 60° C. 90° D. 120°
D
【解析】试题解析：∵|sinA-|+（-tanB）2=0，
∴|sinA-|=0，（ -tanB）2=0，
∴sinA-=0， -tanB=0，
sinA=，tanB=
∴∠A=30°，∠B=30°，
∴∠C=120°．
故选D． 如图，AB∥CD，HP平分∠DHF，若∠AGH=80°，求∠DHP的度数.
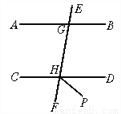
50°
【解析】试题分析：已知AB∥CD，联系平行线的性质不难得到∠EHD的大小，那么∠FHD的大小也就出来了；观察图形，利用角平分线的性质，即可得到∠DHP的大小.
【解析】
∵AB∥CD，
∴∠CHF=∠AGH=80°，
∴∠DHF=180°-80°=100°.
又∵HP平分∠DHF，
∴∠DHP=∠DHF=50°. 下列命题正确的是（ ）
A．内错角相等
B．相等的角是对顶角
C．三条直线相交 ，必产生同位角、内错角、同旁内角
D．同位角相等，两直线平行
D．
【解析】
试题分析：A．只有两直线平行，内错角才相等，故错误；
B．对顶角相等，但相等的角不一定是对顶角，故错误；
C．必须出现“三线八角”的形式，即两直线被第三条直线所截，才产生同位角，内错角，同旁内角，故错误；
D．平行线的判定定理，故正确．
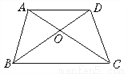
故选D． 如图，AD∥BC，AC与BD相交于O，则图中相等的角有_____对.
四
【解析】∵∠AOB与∠COD是对顶角，∠AOD与∠BOC是对顶角，
∴∠AOB=∠COD，∠AOD=∠BOC.
∵AD∥BC,
∴∠CAD=∠ACB，∠ADB=∠CBD.
∴图中相等的角有四对. 下列语句中，正确的个数有（ ）
①两个关于某直线对称的图形是全等的
②两个图形关于某直线对称，对称点一定在该直线的两旁
③两个成轴对称的图形的对应点连线的垂直平分线，就是它们的对称轴
④平面内两个全等的图形一定关于某直线对称．
A. 1个 B. 2个 C. 3个 D. 4个
B
【解析】【解析】
①两个关于某直线对称的图形是全等的，此选项正确；
②两个图形关于某直线对称，对称点一定在该直线的两旁也有可能在直线上，此选项错误；
③两个成轴对称的图形的对应点连线的垂直平分线，就是它们的对称轴，此选项正确；
④平面内两个全等的图形不一定关于某直线对称，故此选项错误．
故选B． 等腰三角形两边的长分别为2cm和5cm，则这个三角形的周长是( )
A. 9cm B. 12cm C. 9cm和12cm D. 在9cm与12cm之间
B
【解析】【解析】
三角形的周长等于三条边长的和．因为是等腰三角形，因此有两条边相等．所以，三边长可能是：2cm、 2cm、5cm，或者2cm、 5cm、5cm；因为三角形的任意两边之和大于第三边，故2cm、 2cm、5cm不合实际，舍去．所以周长为12cm．故B．