题目内容
如图,直线AB、CD相交于点O,EF⊥AB于O,且∠COE=50°,则∠BOD等于( )
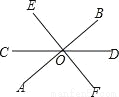
A. 40° B. 45° C. 55° D. 65°
 A
【解析】∵EF⊥AB于O,∠COE=50°,
∴∠AOC=90°-50°=40°,
∵∠AOC与∠BOD是对顶角,
∴∠BOD=∠AOC=40°;
故选A。
A
【解析】∵EF⊥AB于O,∠COE=50°,
∴∠AOC=90°-50°=40°,
∵∠AOC与∠BOD是对顶角,
∴∠BOD=∠AOC=40°;
故选A。
练习册系列答案
 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
如果一个三角形三条高的交点在三角形外部,那么这个三角形是( )
A. 锐角三角形 B. 钝角三角形
C. 直角三角形 D. 无法确定
 B
【解析】试题解析:由题意可知,如果一个三角形的三条高的交点在三角形外部,那么这个三角形是钝角三角形;
故选B.
B
【解析】试题解析:由题意可知,如果一个三角形的三条高的交点在三角形外部,那么这个三角形是钝角三角形;
故选B. 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D.若AC=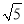 ,BC=2,则sin∠ACD的值为( )
,BC=2,则sin∠ACD的值为( )
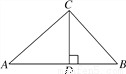
A. 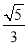 B.
B. 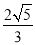 C.
C. 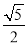 D.
D. 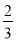
 A
【解析】在Rt△ABC中,根据勾股定理可得:
AB===3.
∵∠B+∠BCD=90°,∠ACD+∠BCD=90°,
∴∠B=∠ACD,
∴sin∠ACD=sin∠B==.
故选A.
A
【解析】在Rt△ABC中,根据勾股定理可得:
AB===3.
∵∠B+∠BCD=90°,∠ACD+∠BCD=90°,
∴∠B=∠ACD,
∴sin∠ACD=sin∠B==.
故选A. 计算6tan45°-2cos60°的结果是()
A. 4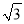 B. 4 C. 5
B. 4 C. 5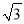 D. 5
D. 5
 D
【解析】试题分析:将特殊角的三角函数值代入计算即可:原式.故选D.
D
【解析】试题分析:将特殊角的三角函数值代入计算即可:原式.故选D. 如图,CD∥AB,∠DCB=70°,∠CBF=20°,∠EFB=130°,问直线EF与AB有怎样的位置关系,为什么?
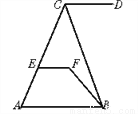
 平行
【解析】试题分析:由CD∥AB,∠DCB=70°可求出∠ABC==70°,进而求出∠ABF=50°,从而可得∠ABF+∠EFB=180°,根据同旁内角互补两直线平行可证EF∥AB.
证明:∵CD∥AB,
∴∠ABC=∠DCB=70°,
∠ABF=∠ABC-∠CBF=70°-20°=50°
∵∠ABF+∠EFB=50°+130°=180°
∴EF∥...
平行
【解析】试题分析:由CD∥AB,∠DCB=70°可求出∠ABC==70°,进而求出∠ABF=50°,从而可得∠ABF+∠EFB=180°,根据同旁内角互补两直线平行可证EF∥AB.
证明:∵CD∥AB,
∴∠ABC=∠DCB=70°,
∠ABF=∠ABC-∠CBF=70°-20°=50°
∵∠ABF+∠EFB=50°+130°=180°
∴EF∥... 下列语句错误的是( )
A. 锐角的补角一定是钝角 B. 一个锐角和一个钝角一定互补
C. 互补的两角不能都是钝角 D. 互余且相等的两角都是45°
 B
【解析】A. ∵锐角小于90°,∴ 锐角的补角一定是钝角,故正确;
B. ∵如:30°+100°=130°,∴一个锐角和一个钝角不一定互补,故不正确;
C. ∵如果两个角都是钝角,则其和就大于180°,∴互补的两角不能都是钝角,故正确;
D. ∵互余且相等的两角都是45°,故正确;
故选B.
B
【解析】A. ∵锐角小于90°,∴ 锐角的补角一定是钝角,故正确;
B. ∵如:30°+100°=130°,∴一个锐角和一个钝角不一定互补,故不正确;
C. ∵如果两个角都是钝角,则其和就大于180°,∴互补的两角不能都是钝角,故正确;
D. ∵互余且相等的两角都是45°,故正确;
故选B. 如图,∠1=82°,∠2=98°,∠3=80°,则∠4的度数为_____.
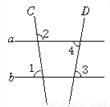
 80°
【解析】
∵∠2=98°,
∴∠5=98°.
∵∠1=82°,
∴∠1+∠5=82°+98°=180°,
∴a∥b,
∵∠3=80°,
∴∠4=∠3=80°.
80°
【解析】
∵∠2=98°,
∴∠5=98°.
∵∠1=82°,
∴∠1+∠5=82°+98°=180°,
∴a∥b,
∵∠3=80°,
∴∠4=∠3=80°. 如图,正六边形ABCDEF关于直线l的轴对称图形是六边形A′B′C′D′E′F′,下列判断错误的是( ).
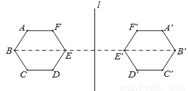
A.AB=A′B′ B.BC∥B′C′ C.直线l⊥BB′ D.∠A′=120°
 B.
【解析】
试题分析:关于轴对称的两个图形沿对称轴翻折,能够重合,两个图形是全等形,对应边相等,所以A正确;C正确,因为正六边形的一个内角是120度,所以D正确.故本题选B.
B.
【解析】
试题分析:关于轴对称的两个图形沿对称轴翻折,能够重合,两个图形是全等形,对应边相等,所以A正确;C正确,因为正六边形的一个内角是120度,所以D正确.故本题选B. 下列图形中,不是轴对称图形的是( )
A. 有两个内角相等的三角形 B. 有一个内角是45°直角三角形
C. 有一个内角是30°的直角三角形 D. 有两个角分别是30°和120°的三角形
 C
【解析】试题分析:因为有两个内角相等的三角形是等腰三角形,是轴对称图形,所以A正确;因为有一个内角是45°直角三角形是等腰直角三角形,是轴对称图形,所以A正确;因为有一个内角是30°的直角三角形,不是轴对称图形,所以C错误;因为有两个角分别是30°和120°的三角形是等腰三角形,是轴对称图形,所以D正确;故选:C.
C
【解析】试题分析:因为有两个内角相等的三角形是等腰三角形,是轴对称图形,所以A正确;因为有一个内角是45°直角三角形是等腰直角三角形,是轴对称图形,所以A正确;因为有一个内角是30°的直角三角形,不是轴对称图形,所以C错误;因为有两个角分别是30°和120°的三角形是等腰三角形,是轴对称图形,所以D正确;故选:C. 
