��Ŀ����
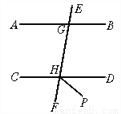
��ͼ��AB��CD��HPƽ�֡�DHF������AGH=80�㣬���DHP�Ķ���.
 50��
�������������������֪AB��CD����ϵƽ���ߵ����ʲ��ѵõ���EHD�Ĵ�С����ô��FHD�Ĵ�СҲ�ͳ����ˣ��۲�ͼ�Σ����ý�ƽ���ߵ����ʣ����ɵõ���DHP�Ĵ�С.
��������
��AB��CD��
���CHF=��AGH=80�㣬
���DHF=180��-80��=100��.
�֡�HPƽ�֡�DHF��
���DHP=��DHF=50��.
50��
�������������������֪AB��CD����ϵƽ���ߵ����ʲ��ѵõ���EHD�Ĵ�С����ô��FHD�Ĵ�СҲ�ͳ����ˣ��۲�ͼ�Σ����ý�ƽ���ߵ����ʣ����ɵõ���DHP�Ĵ�С.
��������
��AB��CD��
���CHF=��AGH=80�㣬
���DHF=180��-80��=100��.
�֡�HPƽ�֡�DHF��
���DHP=��DHF=50��.
 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
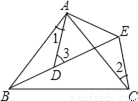
Сѧ��10����Ӧ����ϵ�д���ͼ��ʾ�� AB=AC��AD=AE����BAC=��DAE����1=25�㣬��2=30�㣬���3=_____.
 55��
�������������BAD=��EAC��֤��BAD�ա�EAC���Ƴ���2=��ABD=30�㣬���������ε��������������ɣ�
��������
�ߡ�BAC=��DAE��
���BAC����DAC=��DAE����DAC��
���1=��EAC��
�ڡ�BAD�͡�EAC�У�
AB=AC����BAD=��EAC��
���BAD�ա�EAC��SAS����
���2=��ABD=30�㣬
��...
55��
�������������BAD=��EAC��֤��BAD�ա�EAC���Ƴ���2=��ABD=30�㣬���������ε��������������ɣ�
��������
�ߡ�BAC=��DAE��
���BAC����DAC=��DAE����DAC��
���1=��EAC��
�ڡ�BAD�͡�EAC�У�
AB=AC����BAD=��EAC��
���BAD�ա�EAC��SAS����
���2=��ABD=30�㣬
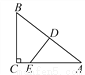
��... ��ͼ������AΪֱ�Ƕ���ĵ���Rt��ABC��ֱ��BCƽ�Ƶõ���A��B��C�䣬ʹ��B����C�غϣ�����A��B����sin��A��BC���ֵΪ_____��cos��A��BC��________��
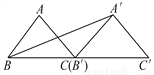
 ����������A������A��D��BC�䣬����ΪD��
�ڵ���ֱ��������A��B��C���У���A��D�ǵױ��ϵ����ߣ�
��B��C��=2 A��D��
��BC=B��C�䣬BD=BC+B��D��
��A��B= ��
�� sin��A��BC��=��cos��A��BC����
�ʴ�Ϊ�� �� .
����������A������A��D��BC�䣬����ΪD��
�ڵ���ֱ��������A��B��C���У���A��D�ǵױ��ϵ����ߣ�
��B��C��=2 A��D��
��BC=B��C�䣬BD=BC+B��D��
��A��B= ��
�� sin��A��BC��=��cos��A��BC����
�ʴ�Ϊ�� �� . ��ͼ����Rt��ABC�У���ACB��90�㣬D��AB���е㣬��D����AB�Ĵ��߽�AC�ڵ�E��BC��6��sinA��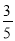 ����DE��____________��
����DE��____________��
 �������������������Rt��ABC�У������AB��AC�̶��ó�AD�����ɡ�ADE�ס�ACB�����ö�Ӧ�߳ɱ��������DE��
�����������BC=6��sinA=��
��AB=10��
��AC=��
��D��AB���е㣬
��AD=AB=5��
�ߡ�ADE�ס�ACB��
�࣬����
��ã�DE=��
����: 1.��ֱ�������Σ�2.�߶δ�ֱƽ���ߵ����ʣ�3���ɶ���.
...
�������������������Rt��ABC�У������AB��AC�̶��ó�AD�����ɡ�ADE�ס�ACB�����ö�Ӧ�߳ɱ��������DE��
�����������BC=6��sinA=��
��AB=10��
��AC=��
��D��AB���е㣬
��AD=AB=5��
�ߡ�ADE�ס�ACB��
�࣬����
��ã�DE=��
����: 1.��ֱ�������Σ�2.�߶δ�ֱƽ���ߵ����ʣ�3���ɶ���.
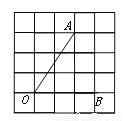
... ��ͼ������AOB������5��5�������������У���sin��AOB��ֵ�ǣ� ��
A��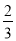 B��
B��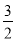 C��
C��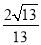 D��
D��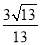
 D��
��������
�����������ֱ�ǡ�OAC�У�OC=2��AC=3����OA===����sin��AOB===����ѡD��
D��
��������
�����������ֱ�ǡ�OAC�У�OC=2��AC=3����OA===����sin��AOB===����ѡD�� ��ͼ����AB��CD�����A����E����D֮��Ĺ�ϵ��( )
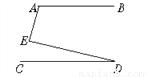
A. ��A+��E+��D=180�� B. ��A����E+��D=180��
C. ��A+��E����D=180�� D. ��A+��E+��D=270��
 C
������������E��EF��CD��
��AB��CD��
��AB��EF��CD��
���AEF=180��-��A,��DEF=��D��
���AED=��AEF+��DEF=180��-��A+��D��
����AED+��A-��D =180��.
��ѡC.
C
������������E��EF��CD��
��AB��CD��
��AB��EF��CD��
���AEF=180��-��A,��DEF=��D��
���AED=��AEF+��DEF=180��-��A+��D��
����AED+��A-��D =180��.
��ѡC. ��ͼ��(1)�ߡ�A=_____(��֪)��
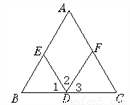
��AC��ED( )
(2)�ߡ�2=_____(��֪)��
��AC��ED( )
(3)�ߡ�A+_____=180��(��֪)��
��AB��FD( )
(4)��AB��_____(��֪)��
���2+��AED=180��( )
(5)��AC��_____(��֪)��
���C=��1( )
 (1)��BED ͬλ�����,��ֱ��ƽ��?
(2)��DFC �ڴ�����ȣ���ֱ��ƽ��?
(3)��AFD ͬ���ڽǻ�������ֱ��ƽ��?
(4)DF ��ֱ��ƽ�У�ͬ���ڽǻ���?
(5)ED ��ֱ��ƽ�У�ͬλ�����
��������(1)��BED ,ͬλ�����,��ֱ��ƽ��?
(2)��DFC ,�ڴ�����ȣ���ֱ��ƽ��?
(3)��AFD ,ͬ���ڽǻ�������ֱ��ƽ��?
(4)...
(1)��BED ͬλ�����,��ֱ��ƽ��?
(2)��DFC �ڴ�����ȣ���ֱ��ƽ��?
(3)��AFD ͬ���ڽǻ�������ֱ��ƽ��?
(4)DF ��ֱ��ƽ�У�ͬ���ڽǻ���?
(5)ED ��ֱ��ƽ�У�ͬλ�����
��������(1)��BED ,ͬλ�����,��ֱ��ƽ��?
(2)��DFC ,�ڴ�����ȣ���ֱ��ƽ��?
(3)��AFD ,ͬ���ڽǻ�������ֱ��ƽ��?
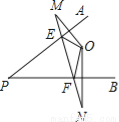
(4)... ��ͼ��ʾ����֪O�ǡ�APB�ڵ�һ�㣬��M��N�ֱ���O�����PA��PB�ĶԳƵ㣬MN��PA��PB�ֱ��ཻ�ڵ�E��F����֪MN=5cm�����OEF���ܳ�Ϊ .
 5cm��
��������
��������� ��O�ǡ�APB�ڵ�һ�㣬��M��N�ֱ���O�����PA��PB�ĶԳƵ㣬��OE=ME��OF=NF��
��MN=5cm�����OEF���ܳ�Ϊ��OE+EF+OF=ME+EF+NF=MN=5��cm�����ʴ�Ϊ��5cm��
5cm��
��������
��������� ��O�ǡ�APB�ڵ�һ�㣬��M��N�ֱ���O�����PA��PB�ĶԳƵ㣬��OE=ME��OF=NF��
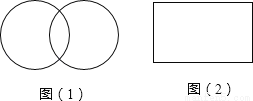
��MN=5cm�����OEF���ܳ�Ϊ��OE+EF+OF=ME+EF+NF=MN=5��cm�����ʴ�Ϊ��5cm�� ��ͼ��1����ͼ��2��������Գ�ͼ�Σ�ͼ��1�����������Գ��ᣬͼ��2�����������Գ���
 2��2
�����������ݶԳ���Ķ��壺���һ��ͼ������һ��ֱ�߶��ۣ������ͼ������ȫ�غϣ����ͼ�ξ�����Գ�ͼ�Σ��ۺ����ڵ�����ֱ�߽����Գ��ᣮ���˶�������������ͼ�ν����ж�
2��2
�����������ݶԳ���Ķ��壺���һ��ͼ������һ��ֱ�߶��ۣ������ͼ������ȫ�غϣ����ͼ�ξ�����Գ�ͼ�Σ��ۺ����ڵ�����ֱ�߽����Գ��ᣮ���˶�������������ͼ�ν����ж� 
