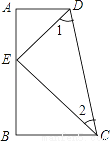
已知:如图,CB⊥AB,CE平分∠BCD,DE平分∠CDA,∠1+∠2=90°,求证:DA⊥AB.
 证明见解析.
【解析】试题分析:根据CE平分∠BCD,DE平分∠CDA,得出∠1+∠2=(∠ADC+∠BCD)=90°,∠ADC+∠BCD=180°,证出AD∥BC,再根据CB⊥AB,即可得出DA⊥AB.
【解析】
∵CE平分∠BCD,DE平分∠CDA,
∴∠1=∠ADC,∠2=∠BCD,
∴∠1+∠2=∠ADC+∠BCD=(∠ADC+∠BCD)=90°,
∴∠AD...
证明见解析.
【解析】试题分析:根据CE平分∠BCD,DE平分∠CDA,得出∠1+∠2=(∠ADC+∠BCD)=90°,∠ADC+∠BCD=180°,证出AD∥BC,再根据CB⊥AB,即可得出DA⊥AB.
【解析】
∵CE平分∠BCD,DE平分∠CDA,
∴∠1=∠ADC,∠2=∠BCD,
∴∠1+∠2=∠ADC+∠BCD=(∠ADC+∠BCD)=90°,
∴∠AD... 在Rt△ABC中,∠C=90°,sinA=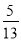 ,则tanA的值为( )
,则tanA的值为( )
A. 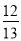 B.
B. 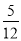 C.
C. 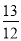 D.
D. 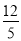
 B
【解析】在△ABC中,∵∠C=90°,∴,又,∴,设BC=5k(k≠0),则AB=13k,∴,∴,故选D.
B
【解析】在△ABC中,∵∠C=90°,∴,又,∴,设BC=5k(k≠0),则AB=13k,∴,∴,故选D. 如图,将∠AOB放置在5×5的正方形网格中,则sin∠AOB的值是( )
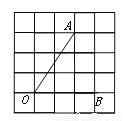
A.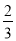 B.
B.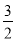 C.
C.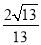 D.
D.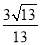
 D.
【解析】
试题分析:在直角△OAC中,OC=2,AC=3,则OA===,则sin∠AOB===.故选D.
D.
【解析】
试题分析:在直角△OAC中,OC=2,AC=3,则OA===,则sin∠AOB===.故选D. 计算6tan45°-2cos60°的结果是()
A. 4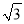 B. 4 C. 5
B. 4 C. 5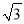 D. 5
D. 5
 D
【解析】试题分析:将特殊角的三角函数值代入计算即可:原式.故选D.
D
【解析】试题分析:将特殊角的三角函数值代入计算即可:原式.故选D. 在△ABC中,若|sinA-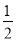 |+(
|+(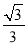 -tanB)2=0,则∠C的度数为( )
-tanB)2=0,则∠C的度数为( )
A. 30° B. 60° C. 90° D. 120°
 D
【解析】试题解析:∵|sinA-|+(-tanB)2=0,
∴|sinA-|=0,( -tanB)2=0,
∴sinA-=0, -tanB=0,
sinA=,tanB=
∴∠A=30°,∠B=30°,
∴∠C=120°.
故选D.
D
【解析】试题解析:∵|sinA-|+(-tanB)2=0,
∴|sinA-|=0,( -tanB)2=0,
∴sinA-=0, -tanB=0,
sinA=,tanB=
∴∠A=30°,∠B=30°,
∴∠C=120°.
故选D. 一斜坡的坡度为1∶3,如果某人站的位置的水平宽度为6米,则他所在的位置的铅直高度为( )
A. 2米 B. 18米 C. 3米 D. 6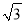 米
米
 A
【解析】设他所在的位置的铅直高度为x米,由题意得
x:6=1:3,
解得:x=2,
故选A.
A
【解析】设他所在的位置的铅直高度为x米,由题意得
x:6=1:3,
解得:x=2,
故选A. 在Rt△ABC中,∠C=90°,下列说法正确的有( )
①sinA>cosA ②sin2A+cos2A=1 ③tanA·tanB=1 ④tanA=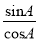
A. ①②③ B. ②③④ C. ①③④ D. ①②③④
 B
【解析】∵∠C=90°,∴,已知中不知BC与AC在大小关系,故①错误;
,故②正确;
,故③正确;
,故④正确,
故选B.
B
【解析】∵∠C=90°,∴,已知中不知BC与AC在大小关系,故①错误;
,故②正确;
,故③正确;
,故④正确,
故选B. 如图,已知l1∥l2∥l3,相邻两条平行直线间的距离相等,若等腰直角△ABC的三个顶点分别在这三条平行直线上,则sina的值是( )
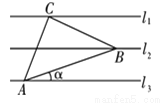
A. 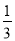 B.
B. 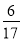 C.
C. 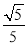 D.
D. 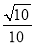
 D
【解析】如图,分别过点A,B作AE⊥l1,BF⊥l1,垂足分别为E,F,BF与l3交于点D,
则易由AAS证明△AEC≌△CFB。
设平行线间距离为d=1,
则CE=BF=1,AE=CF=2,AC=BC=,AB=。
∴。故选D。
D
【解析】如图,分别过点A,B作AE⊥l1,BF⊥l1,垂足分别为E,F,BF与l3交于点D,
则易由AAS证明△AEC≌△CFB。
设平行线间距离为d=1,
则CE=BF=1,AE=CF=2,AC=BC=,AB=。
∴。故选D。 在Rt△ABC中,∠C=90°,AB=2BC,现给出下列结论:①sinA=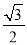 ;②cosB=
;②cosB=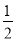 ;③tanA=
;③tanA=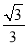 ;④tanB=
;④tanB=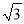 ,其中正确的结论是_____ .
,其中正确的结论是_____ .
 ②③④
【解析】∵在Rt△ABC中,∠C=90°,AB=2BC,∴。∴∠A=30°。∴∠B=60°。
∴cosB= cos60°=,tanA= tan300=,tanB= tan600=。
∴正确的结论是②③④。
②③④
【解析】∵在Rt△ABC中,∠C=90°,AB=2BC,∴。∴∠A=30°。∴∠B=60°。
∴cosB= cos60°=,tanA= tan300=,tanB= tan600=。
∴正确的结论是②③④。 如图,在Rt△ABC中,∠ACB=90°,D是AB的中点,过D点作AB的垂线交AC于点E,BC=6,sinA=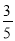 ,则DE=____________.
,则DE=____________.
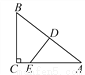
 【解析】试题分析:在Rt△ABC中,先求出AB,AC继而得出AD,再由△ADE∽△ACB,利用对应边成比例可求出DE.
试题解析:∵BC=6,sinA=,
∴AB=10,
∴AC=,
∵D是AB的中点,
∴AD=AB=5,
∵△ADE∽△ACB,
∴,即,
解得:DE=.
考点: 1.解直角三角形;2.线段垂直平分线的性质;3勾股定理.
...
【解析】试题分析:在Rt△ABC中,先求出AB,AC继而得出AD,再由△ADE∽△ACB,利用对应边成比例可求出DE.
试题解析:∵BC=6,sinA=,
∴AB=10,
∴AC=,
∵D是AB的中点,
∴AD=AB=5,
∵△ADE∽△ACB,
∴,即,
解得:DE=.
考点: 1.解直角三角形;2.线段垂直平分线的性质;3勾股定理.
...