题目内容
在Rt△ABC中,∠C=90°,AB=2BC,现给出下列结论:①sinA=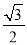 ;②cosB=
;②cosB=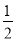 ;③tanA=
;③tanA=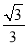 ;④tanB=
;④tanB=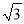 ,其中正确的结论是_____ .
,其中正确的结论是_____ .
 ②③④
【解析】∵在Rt△ABC中,∠C=90°,AB=2BC,∴。∴∠A=30°。∴∠B=60°。
∴cosB= cos60°=,tanA= tan300=,tanB= tan600=。
∴正确的结论是②③④。
②③④
【解析】∵在Rt△ABC中,∠C=90°,AB=2BC,∴。∴∠A=30°。∴∠B=60°。
∴cosB= cos60°=,tanA= tan300=,tanB= tan600=。
∴正确的结论是②③④。
练习册系列答案
 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
如图,在平行四边形纸片上作随机扎针试验,针头扎在阴影区域内的概率为( )

A. 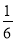 B.
B. 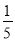 C.
C. 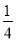 D.
D. 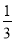
 C
【解析】根据概率公式可得,随机扎针,扎在阴影部分区域的概率= = ,故选C.
C
【解析】根据概率公式可得,随机扎针,扎在阴影部分区域的概率= = ,故选C. 如图,在Rt△ABC和Rt△A′B′C′中,∠C=∠C′=90°,那么在下列各条件中,不能判定Rt△ABC≌Rt△A′B′C′的是( )

A. AB=A′B′=5,BC=B′C′=3 B. AB=B′C′=5,∠A=∠B′=40°
C. AC=A′C′=5,BC=B′C′=3 D. AC=A′C′=5,∠A=∠A′=40°
 B
【解析】∵在Rt△ABC和Rt△A′B′C′中,∠C=∠C′=90°
A选项:AB=A′B′=5,BC=B′C′=3,
符合直角三角形全等的判定条件HL,
∴A选项能使Rt△ABC≌Rt△A′B′C′;
B选项:AB=B′C′=5,∠A=∠B′=40°,
不符合符合直角三角形全等的判定条件,
∴B选项不能使Rt△ABC≌Rt△A′B′C′;
C选项符合Rt△ABC和Rt△A...
B
【解析】∵在Rt△ABC和Rt△A′B′C′中,∠C=∠C′=90°
A选项:AB=A′B′=5,BC=B′C′=3,
符合直角三角形全等的判定条件HL,
∴A选项能使Rt△ABC≌Rt△A′B′C′;
B选项:AB=B′C′=5,∠A=∠B′=40°,
不符合符合直角三角形全等的判定条件,
∴B选项不能使Rt△ABC≌Rt△A′B′C′;
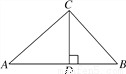
C选项符合Rt△ABC和Rt△A... 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D.若AC=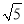 ,BC=2,则sin∠ACD的值为( )
,BC=2,则sin∠ACD的值为( )
A. 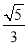 B.
B. 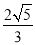 C.
C. 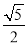 D.
D. 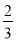
 A
【解析】在Rt△ABC中,根据勾股定理可得:
AB===3.
∵∠B+∠BCD=90°,∠ACD+∠BCD=90°,
∴∠B=∠ACD,
∴sin∠ACD=sin∠B==.
故选A.
A
【解析】在Rt△ABC中,根据勾股定理可得:
AB===3.
∵∠B+∠BCD=90°,∠ACD+∠BCD=90°,
∴∠B=∠ACD,
∴sin∠ACD=sin∠B==.
故选A. 计算:
(1) 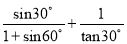 ;
;
(2)tan30°·tan60°+sin245°+cos245°.
 (1) 2;(2)2
【解析】试题分析:(1)、(2)都是把各特殊角的三角函数值代入后,按运算顺序进行计算即可得.
试题解析:(1)原式=;
(2)原式=.
(1) 2;(2)2
【解析】试题分析:(1)、(2)都是把各特殊角的三角函数值代入后,按运算顺序进行计算即可得.
试题解析:(1)原式=;
(2)原式=. 计算6tan45°-2cos60°的结果是()
A. 4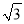 B. 4 C. 5
B. 4 C. 5 D. 5
D. 5
 D
【解析】试题分析:将特殊角的三角函数值代入计算即可:原式.故选D.
D
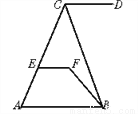
【解析】试题分析:将特殊角的三角函数值代入计算即可:原式.故选D. 如图,CD∥AB,∠DCB=70°,∠CBF=20°,∠EFB=130°,问直线EF与AB有怎样的位置关系,为什么?
 平行
【解析】试题分析:由CD∥AB,∠DCB=70°可求出∠ABC==70°,进而求出∠ABF=50°,从而可得∠ABF+∠EFB=180°,根据同旁内角互补两直线平行可证EF∥AB.
证明:∵CD∥AB,
∴∠ABC=∠DCB=70°,
∠ABF=∠ABC-∠CBF=70°-20°=50°
∵∠ABF+∠EFB=50°+130°=180°
∴EF∥...
平行
【解析】试题分析:由CD∥AB,∠DCB=70°可求出∠ABC==70°,进而求出∠ABF=50°,从而可得∠ABF+∠EFB=180°,根据同旁内角互补两直线平行可证EF∥AB.
证明:∵CD∥AB,
∴∠ABC=∠DCB=70°,
∠ABF=∠ABC-∠CBF=70°-20°=50°
∵∠ABF+∠EFB=50°+130°=180°
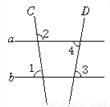
∴EF∥... 如图,∠1=82°,∠2=98°,∠3=80°,则∠4的度数为_____.
 80°
【解析】
∵∠2=98°,
∴∠5=98°.
∵∠1=82°,
∴∠1+∠5=82°+98°=180°,
∴a∥b,
∵∠3=80°,
∴∠4=∠3=80°.
80°
【解析】
∵∠2=98°,
∴∠5=98°.
∵∠1=82°,
∴∠1+∠5=82°+98°=180°,
∴a∥b,
∵∠3=80°,
∴∠4=∠3=80°. 已知a+b=m,ab=-4,化简(a-2)(b-2)的结果是( )
A. 6 B. 2m-8 C. 2m D. -2m
 D
【解析】试题分析:因为(a﹣2)(b﹣2)="ab-2a-2b+4=" ab-2(a+b)+4,且a+b=m,ab=﹣4,所以原式=-4-2m+4=-2m,故选:D.
D
【解析】试题分析:因为(a﹣2)(b﹣2)="ab-2a-2b+4=" ab-2(a+b)+4,且a+b=m,ab=﹣4,所以原式=-4-2m+4=-2m,故选:D. 
