题目内容
一斜坡的坡度为1∶3，如果某人站的位置的水平宽度为6米，则他所在的位置的铅直高度为( )
A. 2米 B. 18米 C. 3米 D. 6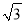
米
A
【解析】设他所在的位置的铅直高度为x米，由题意得
x：6=1：3，
解得：x=2，
故选A.
练习册系列答案
期末好成绩系列答案
99加1领先期末特训卷系列答案
百强名校期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案
金状元绩优好卷系列答案
相关题目
如图，房间内有一架梯子斜靠在墙上，梯子顶端距地面的垂直距离MA为a米，此时梯子的倾斜角为75°，若梯子斜靠在另一面墙时，顶端距地面的垂直距离NB为b米，梯子的倾斜角为45°，则这个房间的宽AB是多少米？为什么？
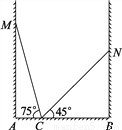
a米．
【解析】试题分析：连结BM、MN，由SSS证明≌，可得∠CBM=∠NBM=45°，AB=AM=a.
试题解析：a米．连结BM、MN，
在△MCN中，∠MCN=180°－75°－45°=60°，CM=CN，
∴△MCN是等边三角形，
∴MC=MN，∠CBN=90°，∠BCN=45°，
∴BC=BN，在△MCB和△MNB中，
∴△MCB≌△MNB，
... 如图，在△ABC中，AD⊥BC于D，BE⊥AC于E，AD与BE相交于点F，若BF=AC，则∠ABC＝______度．
45
【解析】试题分析：根据三角形全等的判定和性质，先证△ADC≌△BDF，可得BD=AD，再根据等腰直角三角形的性质可求∠ABC=∠BAD=45°．
【解析】
∵AD⊥BC于D，BE⊥AC于E
∴∠EAF+∠AFE=90°,∠DBF+∠BFD=90°，
又∵∠BFD=∠AFE(对顶角相等)
∴∠EAF=∠DBF，
在Rt△ADC和Rt△BDF中，
，
... 如图，直线y＝2x＋2与y轴交于A点，与反比例函数y＝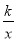
(x＞0)的图象交于点M，过M作MH⊥x轴于点H，且tan∠AHO＝2.
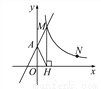
(1)求k的值；
(2)点N(a，1)是反比例函数y＝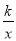
(x＞0)图象上的点，在x轴上是否存在点P，使得PM＋PN最小？若存在，求出点P的坐标；若不存在，请说明理由．
（1）4；（2）P(，0)
【解析】试题分析：（1）根据直线解析式求A点坐标，得OA的长度；根据三角函数定义可求OH的长度，得点M的横坐标；根据点M在直线上可求点M的坐标．从而可求K的值；
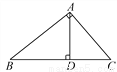
（2）根据反比例函数解析式可求N点坐标；作点N关于x轴的对称点N1，连接MN1与x轴的交点就是满足条件的P点位置． 如图，Rt△ABC中，∠A＝90°，AD⊥BC于点D，若BD∶CD＝3∶2，则tan∠B＝_____________．
,
【解析】∵BD：CD=3：2，∴不妨取BD=3，CD=2，
∵Rt△ABC中，∠A=90°，AD⊥BC于点D，∴AD2=BD•CD=6，解得AD＝，
∴tanB＝，
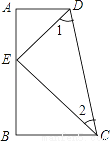
故答案为： ． 已知：如图，CB⊥AB，CE平分∠BCD，DE平分∠CDA，∠1+∠2=90°，求证：DA⊥AB．
证明见解析.
【解析】试题分析：根据CE平分∠BCD，DE平分∠CDA，得出∠1+∠2=（∠ADC+∠BCD）=90°，∠ADC+∠BCD=180°，证出AD∥BC，再根据CB⊥AB，即可得出DA⊥AB．
【解析】
∵CE平分∠BCD，DE平分∠CDA，
∴∠1=∠ADC，∠2=∠BCD，
∴∠1+∠2=∠ADC+∠BCD=（∠ADC+∠BCD）=90°，
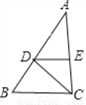
∴∠AD... 如图，CD平分∠ACB，DE∥BC，∠AED=80°，求∠EDC的度数．
40°
【解析】试题分析：根据平行线的性质求出∠ACB的度数，根据角平分线定义求出即可.
试题解析：
∵ DE∥BC，∠AED =80°，∴ ∠EDC =∠BCD，∠ACB=∠AED=80°
∵ CD平分∠ACB，
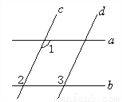
∴ ∠BCD= ∠ACB=40°，∴ ∠EDC=∠BCD=40° 如图，已知直线a∥b,c∥d，∠1=115°，则∠2=_____，∠3=_____.
115° 115°
【解析】∵a∥b,∠1=115°，
∴∠2=∠1=115°.
∵c∥d，
∴∠3=∠2=115°. 下列运算正确的是( )
A. x2＋x2＝x4 B. (a－b)2＝a2－b2 C. (－a2)3＝－a6 D. 3a2·2a3＝6a6
C
【解析】试题分析：A、x2+x2=2x2，故错误；B、（a-b）2=a2-2ab+b2，故错误；C、（-a2）3=-a6，正确；D、3a2·2a3=6a5，故错误；
故选C．