题目内容
如图,在Rt△ABC中,∠ACB=90°,D是AB的中点,过D点作AB的垂线交AC于点E,BC=6,sinA=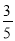 ,则DE=____________.
,则DE=____________.
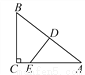
 【解析】试题分析:在Rt△ABC中,先求出AB,AC继而得出AD,再由△ADE∽△ACB,利用对应边成比例可求出DE.
试题解析:∵BC=6,sinA=,
∴AB=10,
∴AC=,
∵D是AB的中点,
∴AD=AB=5,
∵△ADE∽△ACB,
∴,即,
解得:DE=.
考点: 1.解直角三角形;2.线段垂直平分线的性质;3勾股定理.
...
【解析】试题分析:在Rt△ABC中,先求出AB,AC继而得出AD,再由△ADE∽△ACB,利用对应边成比例可求出DE.
试题解析:∵BC=6,sinA=,
∴AB=10,
∴AC=,
∵D是AB的中点,
∴AD=AB=5,
∵△ADE∽△ACB,
∴,即,
解得:DE=.
考点: 1.解直角三角形;2.线段垂直平分线的性质;3勾股定理.
...
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
2014年3月,YC市举办了首届中学生汉字听写大会,从甲、乙、丙、丁4套题中随机抽取一套训练,抽中甲的概率是( )
A. 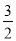 B.
B. 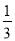 C.
C. 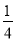 D.
D. 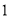
 C
【解析】试题分析:根据概率的求法,找准两点:①全部等可能情况的总数;②符合条件的情况数目;二者的比值就是其发生的概率. 因此,
∵从甲、乙、丙、丁4套题中随机抽取一套训练,∴抽中甲的概率是.故选C.
C
【解析】试题分析:根据概率的求法,找准两点:①全部等可能情况的总数;②符合条件的情况数目;二者的比值就是其发生的概率. 因此,
∵从甲、乙、丙、丁4套题中随机抽取一套训练,∴抽中甲的概率是.故选C. 在两个直角三角形中,若有一对角(非直角)相等,一对边相等,则两个直角三角形( )
A. 一定全等 B. 一定不全等 C. 不一定全等 D. 以上都不是
 C
【解析】如果有一对角(非直角)对应相等,一对边对应相等,题中还隐含着一对直角相等,则这两个三角形一定全等,
若不是对应相等,则不一定全等,
故选C.
C
【解析】如果有一对角(非直角)对应相等,一对边对应相等,题中还隐含着一对直角相等,则这两个三角形一定全等,
若不是对应相等,则不一定全等,
故选C. 如图,菱形ABCD的周长为20cm,DE⊥AB,垂足为E,cosA=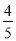 ,则下列结论中正确的个数为( )
,则下列结论中正确的个数为( )
①DE=3cm;②EB=1cm;③S菱形ABCD=15cm2
.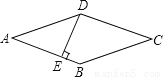
A.3个 B.2个 C.1个 D.0个
 A.
【解析】
试题解析:由题意可得,菱形的边长为5cm,又cosA=,所以AE=4,
则DE=3cm;EB=1cm;S菱形ABCD=5×3=15cm2,
故选A.
A.
【解析】
试题解析:由题意可得,菱形的边长为5cm,又cosA=,所以AE=4,
则DE=3cm;EB=1cm;S菱形ABCD=5×3=15cm2,
故选A. 如图,在△ABC中,CD⊥AB,垂足为点D.若AB=12,CD=6,tanA=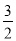 ,求sinB+cosB的值.
,求sinB+cosB的值.
 .
【解析】试题分析:先在Rt△ACD中,由正切函数的定义得tanA==,求出AD=4,则BD=AB﹣AD=8,再解Rt△BCD,由勾股定理得BC==10,sinB==,cosB==,由此求出sinB+cosB=.
【解析】
在Rt△ACD中,∵∠ADC=90°,
∴tanA===,
∴AD=4,
∴BD=AB﹣AD=12﹣4=8.
在Rt△BCD中,∵∠BD...
.
【解析】试题分析:先在Rt△ACD中,由正切函数的定义得tanA==,求出AD=4,则BD=AB﹣AD=8,再解Rt△BCD,由勾股定理得BC==10,sinB==,cosB==,由此求出sinB+cosB=.
【解析】
在Rt△ACD中,∵∠ADC=90°,
∴tanA===,
∴AD=4,
∴BD=AB﹣AD=12﹣4=8.
在Rt△BCD中,∵∠BD... 在△ABC中,若|sinA-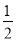 |+(
|+(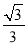 -tanB)2=0,则∠C的度数为( )
-tanB)2=0,则∠C的度数为( )
A. 30° B. 60° C. 90° D. 120°
 D
【解析】试题解析:∵|sinA-|+(-tanB)2=0,
∴|sinA-|=0,( -tanB)2=0,
∴sinA-=0, -tanB=0,
sinA=,tanB=
∴∠A=30°,∠B=30°,
∴∠C=120°.
故选D.
D
【解析】试题解析:∵|sinA-|+(-tanB)2=0,
∴|sinA-|=0,( -tanB)2=0,
∴sinA-=0, -tanB=0,
sinA=,tanB=
∴∠A=30°,∠B=30°,
∴∠C=120°.
故选D. 如图,AB∥CD,HP平分∠DHF,若∠AGH=80°,求∠DHP的度数.
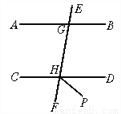
 50°
【解析】试题分析:已知AB∥CD,联系平行线的性质不难得到∠EHD的大小,那么∠FHD的大小也就出来了;观察图形,利用角平分线的性质,即可得到∠DHP的大小.
【解析】
∵AB∥CD,
∴∠CHF=∠AGH=80°,
∴∠DHF=180°-80°=100°.
又∵HP平分∠DHF,
∴∠DHP=∠DHF=50°.
50°
【解析】试题分析:已知AB∥CD,联系平行线的性质不难得到∠EHD的大小,那么∠FHD的大小也就出来了;观察图形,利用角平分线的性质,即可得到∠DHP的大小.
【解析】
∵AB∥CD,
∴∠CHF=∠AGH=80°,
∴∠DHF=180°-80°=100°.
又∵HP平分∠DHF,
∴∠DHP=∠DHF=50°. 如图,AD∥BC,AC与BD相交于O,则图中相等的角有_____对.
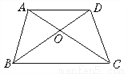
 四
【解析】∵∠AOB与∠COD是对顶角,∠AOD与∠BOC是对顶角,
∴∠AOB=∠COD,∠AOD=∠BOC.
∵AD∥BC,
∴∠CAD=∠ACB,∠ADB=∠CBD.
∴图中相等的角有四对.
四
【解析】∵∠AOB与∠COD是对顶角,∠AOD与∠BOC是对顶角,
∴∠AOB=∠COD,∠AOD=∠BOC.
∵AD∥BC,
∴∠CAD=∠ACB,∠ADB=∠CBD.
∴图中相等的角有四对. 若3x=4,9y=7,则3x-2y的值为( )
A.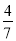 B.
B.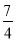 C.-3 D.
C.-3 D.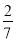
 A
【解析】
由3x=4,9y=7与3x-2y=3x÷32y=3x÷(32)y,代入即可求得答案.
A
【解析】
由3x=4,9y=7与3x-2y=3x÷32y=3x÷(32)y,代入即可求得答案. 
