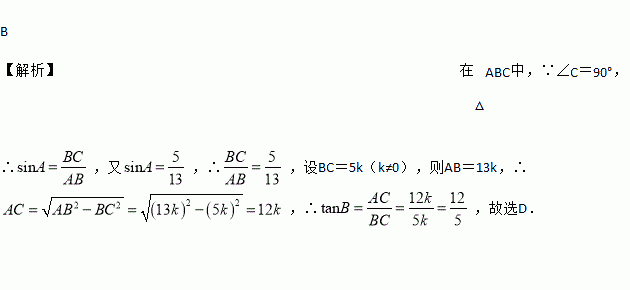题目内容
在Rt△ABC中,∠C=90°,sinA=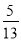 ,则tanA的值为( )
,则tanA的值为( )
A. 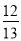 B.
B. 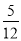 C.
C. 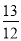 D.
D. 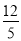
 B
【解析】在△ABC中,∵∠C=90°,∴,又,∴,设BC=5k(k≠0),则AB=13k,∴,∴,故选D.
B
【解析】在△ABC中,∵∠C=90°,∴,又,∴,设BC=5k(k≠0),则AB=13k,∴,∴,故选D.
练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
如图所示,太阳光线AC与A′C′是平行的,AB表示一棵塔松,A′B′表示一棵小杨树,同一时刻两棵树的影长相等,已知塔松高6米,则小杨树高______.
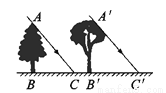
 6米
【解析】试题解析:∵ AC∥A′C′
∴∠ACB=∠A′C′B′(两直线平行,同位角相等)
∵ 树木是垂直地面生长的,
∴∠ABC=∠A′B′C′=90°,
∵∠ABC=∠A′B′C′,∠ACB=∠A′C′B′,AC∥A′C′,
∴△ABC≌△A′B′C′(两角及其夹边对应相等的两个三角形全等),
∴AB=A′B′=6米 (全等三角形的对应边相等),...
6米
【解析】试题解析:∵ AC∥A′C′
∴∠ACB=∠A′C′B′(两直线平行,同位角相等)
∵ 树木是垂直地面生长的,
∴∠ABC=∠A′B′C′=90°,
∵∠ABC=∠A′B′C′,∠ACB=∠A′C′B′,AC∥A′C′,
∴△ABC≌△A′B′C′(两角及其夹边对应相等的两个三角形全等),
∴AB=A′B′=6米 (全等三角形的对应边相等),... 如图,在Rt△ABC中,∠ACB=90°,D是边AB的中点,BE⊥CD,垂足为点E.已知AC=15,cosA= .
.
(1)求线段CD的长;
(2)求sin∠DBE的值.
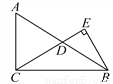
 (1)CD=;(2)sin∠DBE=.
【解析】试题分析:(1)根据直角三角形斜边上的中线等于斜边的一半,求出AB的长,即可求出CD的长;(2)由于D为AB上的中点,求出AD=BD=CD=,设DE=x,EB=y,利用勾股定理即可求出x的值,据此解答即可.
试题解析::【解析】
(1)∵AC=15,cosA=,
∴cosA=,
∴AB=25,
∵△ACB为直角三角形,...
(1)CD=;(2)sin∠DBE=.
【解析】试题分析:(1)根据直角三角形斜边上的中线等于斜边的一半,求出AB的长,即可求出CD的长;(2)由于D为AB上的中点,求出AD=BD=CD=,设DE=x,EB=y,利用勾股定理即可求出x的值,据此解答即可.
试题解析::【解析】
(1)∵AC=15,cosA=,
∴cosA=,
∴AB=25,
∵△ACB为直角三角形,... 计算:
(1) 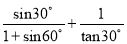 ;
;
(2)tan30°·tan60°+sin245°+cos245°.
 (1) 2;(2)2
【解析】试题分析:(1)、(2)都是把各特殊角的三角函数值代入后,按运算顺序进行计算即可得.
试题解析:(1)原式=;
(2)原式=.
(1) 2;(2)2
【解析】试题分析:(1)、(2)都是把各特殊角的三角函数值代入后,按运算顺序进行计算即可得.
试题解析:(1)原式=;
(2)原式=. 在Rt△ABC中,∠C=90°,下列说法正确的有( )
①sinA>cosA ②sin2A+cos2A=1 ③tanA·tanB=1 ④tanA=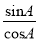
A. ①②③ B. ②③④ C. ①③④ D. ①②③④
 B
【解析】∵∠C=90°,∴,已知中不知BC与AC在大小关系,故①错误;
,故②正确;
,故③正确;
,故④正确,
故选B.
B
【解析】∵∠C=90°,∴,已知中不知BC与AC在大小关系,故①错误;
,故②正确;
,故③正确;
,故④正确,
故选B. 如图,CD∥AB,∠DCB=70°,∠CBF=20°,∠EFB=130°,问直线EF与AB有怎样的位置关系,为什么?
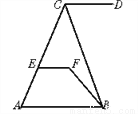
 平行
【解析】试题分析:由CD∥AB,∠DCB=70°可求出∠ABC==70°,进而求出∠ABF=50°,从而可得∠ABF+∠EFB=180°,根据同旁内角互补两直线平行可证EF∥AB.
证明:∵CD∥AB,
∴∠ABC=∠DCB=70°,
∠ABF=∠ABC-∠CBF=70°-20°=50°
∵∠ABF+∠EFB=50°+130°=180°
∴EF∥...
平行
【解析】试题分析:由CD∥AB,∠DCB=70°可求出∠ABC==70°,进而求出∠ABF=50°,从而可得∠ABF+∠EFB=180°,根据同旁内角互补两直线平行可证EF∥AB.
证明:∵CD∥AB,
∴∠ABC=∠DCB=70°,
∠ABF=∠ABC-∠CBF=70°-20°=50°
∵∠ABF+∠EFB=50°+130°=180°
∴EF∥... 如果∠1与∠2互补,∠1与∠3互余,那么 ( )
A. ∠2>∠3 B. ∠2=∠3 C. ∠2<∠3 D. ∠2≥∠3
 A
【解析】∵∠1与∠2互补,∴∠1+∠2=180°,
∵∠1与∠3互余,∴∠1+∠3=90°,
∴∠1+∠2-(∠1+∠3)=180°-90°,
∴∠2-∠3=90°,
∴∠2>∠3.
故选A.
A
【解析】∵∠1与∠2互补,∴∠1+∠2=180°,
∵∠1与∠3互余,∴∠1+∠3=90°,
∴∠1+∠2-(∠1+∠3)=180°-90°,
∴∠2-∠3=90°,
∴∠2>∠3.
故选A. 两条直线相交,有_____对对顶角,三条直线两两相交,有_____对对顶角.
 两 六
【解析】两条直线相交,有两对对顶角,三条直线两两相交,有六对对顶角.
两 六
【解析】两条直线相交,有两对对顶角,三条直线两两相交,有六对对顶角. 下面两个轴对称图形分别只画出一半.请画出它的另一半.(直线l为对称轴)
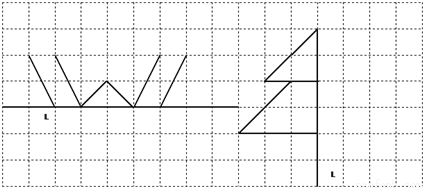
 图形见解析
【解析】试题分析:从各关键点向对称轴引垂线并延长相同单位得到各点的对应点,顺次连接即可.
试题解析:【解析】
所作图形如下:
图形见解析
【解析】试题分析:从各关键点向对称轴引垂线并延长相同单位得到各点的对应点,顺次连接即可.
试题解析:【解析】
所作图形如下: