题目内容
计算6tan45°－2cos60°的结果是()
A. 4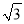
B. 4 C. 5
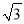D. 5
D
【解析】试题分析：将特殊角的三角函数值代入计算即可：原式．故选D．
练习册系列答案
相关题目
已知△ABC.求作：△A′B′C′，使△A′B′C′≌△ABC.
作图见解析
【解析】试题分析：本题可利用全等三角形的判定定理SSS作图，作AC=A′C′，A′B′=AB，BC=B′C′；根据全等三角形的判定可得△A′B′C′≌△ABC，注意尺规作图中作一条线段等于已知线段的作法．
试题解析：作法：①任意作一条射线B′M，以点B′为圆心，以BC为半径画弧，交射线于点C′；
②分别以点B′和点C′为圆心，以AB和AC为半径画弧，交于点A′，连接A... 如图，∠C＝∠D＝90°，若添加一个条件，可使用“HL”判定Rt△ABC与Rt△ABD全等，则以下给出的条件适合的是( )
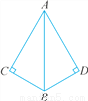
A. AC＝AD B. AB＝AB C. ∠ABC＝∠ABD D. ∠BAC＝∠BAD
A
【解析】根据题意可知∠C=∠D=90°，AB=AB，
然后由AC=AD，可根据HL判定两直角三角形全等，故符合条件；
而B答案只知道一边一角，不能够判定两三角形全等，故不正确；
C答案符合AAS，证明两三角形全等，故不正确；
D答案是符合AAS，能证明两三角形全等，故不正确.
故选：A. 如图，矩形ABCD中，AB＝2AD，E为AD的中点，EF⊥EC交AB于点F，连接FC.
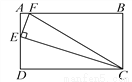
(1)求证：△AEF∽△DCE；
(2)求tan∠ECF的值．
（1）答案见解析；（2）
【解析】（1）根据矩形的性质可知∠A="∠D" =90°，再根据三角形的内角和为180°，可知∠DCE+∠DEC=900，由已知EF⊥EC，可得：∠AEF+∠DEC=900得出∠DCE=∠AEF，即可证明⊿AEF∽⊿DCE
（2）由（1）可知：⊿AEF∽⊿DCE ∴=
在矩形ABCD中，E为AD 的中点。
AB=2AD ∴ DC=AB=4AE ∴ ... 在Rt△ABC中，∠C＝90°，AB＝2BC，现给出下列结论：①sinA＝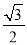
；②cosB＝
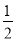；③tanA＝
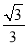；④tanB＝
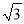，其中正确的结论是_____ .
②③④
【解析】∵在Rt△ABC中，∠C=90°，AB=2BC，∴。∴∠A=30°。∴∠B=60°。
∴cosB= cos60°=，tanA= tan300=，tanB= tan600=。
∴正确的结论是②③④。 根据下列证明过程填空：
如图，已知BD⊥AC，EF⊥AC，D、F分别为垂足，且∠1=∠4，求证：∠ADG=∠C
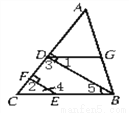
证明：∵BD⊥AC，EF⊥AC
∴∠2=∠3=90°（ ）
∴BD∥EF ( )
∴∠4=_____( )
∵∠1=∠4
∴∠1=_____( )
∴DG∥BC( )
∴∠ADG=∠C( )
见解析
【解析】试题分析：解决问题要熟悉平行线的性质和判定，能正确运用语言叙述理由，还要注意平行线的性质和判定的综合运用．
试题解析：∵BD⊥AC，EF⊥AC（已知），
∴∠2=∠3=90°，
∴BD∥EF（同位角相等，两直线平行），
∴∠4=∠5（两直线平行，同位角相等）；
∵∠1=∠4（已知），
∴∠1=∠5（等量代换），
∴DG∥BC（内错角相... 如图，直线AB、CD相交于点O，EF⊥AB于O，且∠COE=50°，则∠BOD等于（ ）
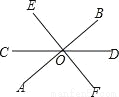
A. 40° B. 45° C. 55° D. 65°
A
【解析】∵EF⊥AB于O，∠COE=50°，
∴∠AOC=90°-50°=40°，
∵∠AOC与∠BOD是对顶角，
∴∠BOD=∠AOC=40°；
故选A。 已知∠AOB=40°，OC平分∠AOB，则∠AOC的补角等于_____.
160°
【解析】
∵OC平分∠AOB，∠AOB=40°，
∴,
∴∠AOC的补角=180°-20°=160°. 如图，已知点P是∠AOB平分线上一点，PC⊥OA，PD⊥OB，垂足为C，D.
(1)∠PCD＝∠PDC吗？为什么？
(2)OP是CD的垂直平分线吗？为什么？
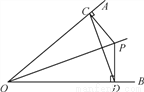
（1）见解析；（2）见解析
【解析】试题分析：（1）由角平分线的性质易得PC=PD，根据等边对等角即可得出∠PCD=∠PDC；
（2）易证△POC≌△POD，则OC=OD，根据线段垂直平分线的性质逆定理可得OP垂直平分CD．
试题解析：（1）∠PCD＝∠PDC，理由如下：
∵点P是∠AOB平分线上一点，PC⊥OA，PD⊥OB，
∴PC＝PD，
∴∠PCD＝∠PD...