题目内容
在△ABC中，若|sinA－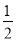
|＋(
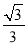－tanB)2＝0，则∠C的度数为( )
A. 30° B. 60° C. 90° D. 120°
D
【解析】试题解析：∵|sinA-|+（-tanB）2=0，
∴|sinA-|=0，（ -tanB）2=0，
∴sinA-=0， -tanB=0，
sinA=，tanB=
∴∠A=30°，∠B=30°，
∴∠C=120°．
故选D．
如图，已知在△ABC中，AD⊥BC于点D，AE平分∠BAC，判断∠EAD与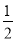
(∠C－∠B)的关系，并说明理由．
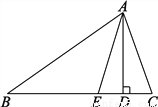
∠EAD= (∠C－∠B)．理由见解析
【解析】试题分析：根据三角形内角和定理求出求出∠DAC和∠EAC，相减即可得出答案．
试题解析：
理由是：
∵AE平分∠BAC，
∵AD⊥BC， 如图所示，在Rt△ACD和Rt△BCE中，若AD＝BE，DC＝EC，则无法得出的结论是( )
A. OA＝OB B. E是AC的中点 C. △AOE≌△BOD D. AE＝BD
B
【解析】∵∠C=∠C=90°，
∴△ACD和△BCE是直角三角形，
在Rt△ACD和Rt△BCE中，
∴Rt△ACD≌Rt△BCE（HL），
∴∠B=∠A，CB=CA，
∵CD=CE，
∴AE=BD，故D正确，
在△AOE和△BOD中，
∴△AOE≌△BOD（AAS），故C正确，
∴AO=OB，故A正确，
AE=BD，CE=CD... 阅读下面的材料，再回答问题：
三角函数中常用公式sin(A＋B)＝sinAcosB＋cosAsinB，求sin(A＋B)的值．
例如：sin75°＝sin(45°＋30°)＝sin45°cos30°＋cos45°sin30°＝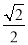
×
＋
×
＝
＋
＝
.
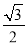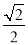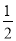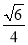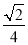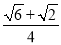试用公式cos(A＋B)＝cosAcosB－sinAsinB，求cos75°的值．
【解析】试题分析：将cos75°变为cos(45°+30°)，然后按所给的公式进行计算即可.
试题解析：cos75°＝cos(45°＋30°)＝cos45°cos30°－sin45°sin30°=. 如图，在Rt△ABC中，∠ACB＝90°，D是AB的中点，过D点作AB的垂线交AC于点E，BC＝6，sinA＝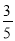
，则DE＝____________．
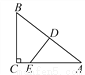
【解析】试题分析：在Rt△ABC中，先求出AB，AC继而得出AD，再由△ADE∽△ACB，利用对应边成比例可求出DE．
试题解析：∵BC=6，sinA=，
∴AB=10，
∴AC=，
∵D是AB的中点，
∴AD=AB=5，
∵△ADE∽△ACB，
∴，即，
解得：DE=．
考点: 1.解直角三角形；2.线段垂直平分线的性质；3勾股定理.
... 阅读下面的证明过程，指出其错误.
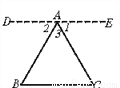
已知△ABC
求证：∠A+∠B+∠C=180°
证明：过A作DE∥BC，且使∠1=∠C
∵DE∥BC(画图)
∴∠2=∠B(两直线平行，内错角相等)
∵∠1=∠C(画图)
∴∠B+∠C+∠3=∠2+∠1+∠3=180°
即∠BAC+∠B+∠C=180°
答案见解析
【解析】试题分析：注意作辅助线的方法，过点A作的辅助线不能同时满足两个条件．只能作平行线后，根据平行线的性质得到∠1=∠C．
错误①：过A作DE∥BC，且使∠1=∠C，应改为：过A作DE∥BC.
错误②：∵∠1=∠C(画图)，理由错，应改为：两直线平行，内错角相等. 如图，若AB∥CD，则∠A、∠E、∠D之间的关系是( )
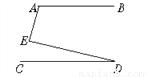
A. ∠A+∠E+∠D=180° B. ∠A－∠E+∠D=180°
C. ∠A+∠E－∠D=180° D. ∠A+∠E+∠D=270°
C
【解析】过点E作EF∥CD，
∵AB∥CD，
∴AB∥EF∥CD，
∴∠AEF=180°-∠A,∠DEF=∠D，
∴∠AED=∠AEF+∠DEF=180°-∠A+∠D；
即∠AED+∠A-∠D =180°.
故选C. 如图，若l1∥l2，∠1=45°，则∠2=_____.
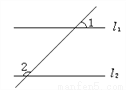
135
【解析】试题分析：根据对顶角的性质求出∠1的对顶角，然后根据两直线平行同旁内角互补得出∠2的度数. 如图，EFGH为矩形台球桌面，现有一白球A和一彩球B.应怎样击打白球A,才能使白球A碰撞台边EF,反弹后能击中彩球B?通过作图，指出A球运行路线.
图形见解析
【解析】试题分析：找到A球关于EF的对称点A′，连接BA′，则BA′与EF交点即为台球的撞击点．
试题解析：【解析】
如图，作点A关于EF的对称点A′，连接A′B，交EF于点C，将白球A打到台边EF的点C处，反弹后能击中彩球B．