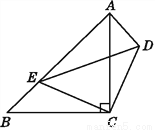
如图,△ABC,△CDE均为等腰直角三角形,∠ACB=∠DCE=90°,点E在AB上,试说明:△CDA≌△CEB.
答案见解析
【解析】试题分析：根据等腰直角三角形的性质得出CE=CD，BC=AC，再利用全等三角形的判定证明即可．
试题解析：证明：∵△ABC、△CDE均为等腰直角三角形，∠ACB=∠DCE=90°，
∴CE=CD，BC=AC，
∴∠ACB﹣∠ACE=∠DCE﹣∠ACE，
∴∠ECB=∠DCA，
在△CDA与△CEB中， ，
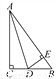
∴△CDA≌△CEB． 如图，在△ABC中，∠C＝90°，D为BC上一点，且DE⊥AB于E，AC＝AE.求证：AD平分∠BAC.
见解析
【解析】试题分析：证明Rt△ACD≌Rt△AED，利用全等三角形的性质即可得.
试题解析：∵DE⊥AB，∴∠AED=90°，
在Rt△ACD和Rt△AED中，
，
∴Rt△ACD≌Rt△AED（HL），
∴∠CAD=∠EAD，
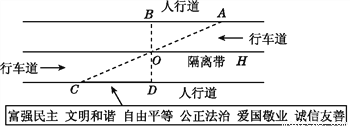
即AD平分∠BAC. 杨阳同学沿一段笔直的人行道行走,在由A步行到达B处的过程中,通过隔离带的空隙O,刚好浏览完对面人行道宣传墙上的社会主义核心价值观标语,其具体信息汇集如下:
如图,AB∥OH∥CD,相邻两平行线间的距离相等,AC,BD相交于O,OD⊥CD,垂足为D,已知AB=20米,请根据上述信息求标语CD的长度.
20米.
【解析】试题分析：已知AB∥CD，根据平行线的性质可得∠ABO=∠CDO，再由垂直的定义可得∠CDO=90°，可得OB⊥AB，根据相邻两平行线间的距离相等可得OD=OB，即可根据ASA定理判定△ABO≌△CDO，由全等三角形的性质即可得CD=AB=20m．
试题解析：∵AB∥CD，∴∠ABO=∠CDO，
∵OD⊥CD，∴∠CDO=90°，
∴∠ABO=90°，即O... （2011•江津区）在△ABC中，AB=CB，∠ABC=90°，F为AB延长线上一点，点E在BC上，且AE=CF．
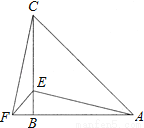
（1）求证：Rt△ABE≌Rt△CBF；
（2）若∠CAE=30°，求∠ACF的度数．
（1）见解析；（2）60°．
【解析】
试题分析：（1）由AB=CB，∠ABC=90°，AE=CF，即可利用HL证得Rt△ABE≌Rt△CBF；
（2）由AB=CB，∠ABC=90°，即可求得∠CAB与∠ACB的度数，即可得∠BAE的度数，又由Rt△ABE≌Rt△CBF，即可求得∠BCF的度数，则由∠ACF=∠BCF+∠ACB即可求得答案．
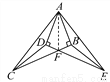
（1）证明：∵∠ABC=90°，... 如图，∠ABC＝∠ADE＝90°，AD＝AB，AC＝AE，BC与DE相交于点F，连接CD、EB.
(1)图中共有几对全等三角形，请你一一列举；
(2)求证：CF＝EF.
（1）有三对全等三角形，具体见解析；（2）证明见解析.
【解析】试题分析：（1）根据全等三角形的判定，结合图形得出即可；
（2）连接AF，根据HL证Rt△ABC≌Rt△ADE推出BC=DE，根据HL推出△ADF≌△ABF，推出DF=BF，利用线段的差即可得.
试题解析：(1) 图中有3对全等三角形有Rt△ABC≌Rt△ADE，△ACD≌△AEB，△CDF≌△EBF；
(2)... 下列说法中:
①P是线段AB上的一点,直线l经过点P且l⊥AB,则l是线段AB的垂直平分线;
②直线l经过线段AB的中点,则l是线段AB的垂直平分线;
③若AP=PB,且直线l垂直于线段AB,则l是线段AB的垂直平分线;
④经过线段AB的中点P且垂直于AB的直线l是线段AB的垂直平分线.
其中正确的有( )
A. 1个 B. 2个 C. 3个 D. 4个
A
【解析】根据线段的垂直平分线的定义，以及定理：到线段的两端距离相等的点在线段的垂直平分线上，即可判断．
【解析】
①当P不是AB的中点，则直线l不平分线段AB，故错误；
②直线l经过线段AB的中点，且垂直于AB则l是线段AB的垂直平分线，故错误；
③若AP=PB，则P在线段AB的垂直平分线上，但l不一定过点P，所以直线l不一定是线段AB的垂直平分线，故错误；
④... 关于线段的垂直平分线有以下说法:
①一条线段的垂直平分线的垂足,也是这条线段的中点;
②线段的垂直平分线是一条直线;
③一条线段的垂直平分线是这条线段的唯一对称轴.
其中正确的说法有( )
A. 1个 B. 2个 C. 3个 D. 0个
B
【解析】由线段垂直平分线的定义，可得一条线段的垂直平分线的垂足，也是这条线段的中点；线段的垂直平分线是一条直线．注意举反例来判断．
【解析】
①一条线段的垂直平分线的垂足，也是这条线段的中点，正确；
②线段的垂直平分线是一条直线；正确；
③一条线段的垂直平分线是这条线段的唯一对称轴，错误，因为线段有2条对称轴：一条是这条线段的垂直平分线，另一条对称轴是这条线段所在的直... 已知△ABC的周长是l,BC=l-2AB,则下列直线一定为△ABC的对称轴的是( )
A. △ABC的边AB的垂直平分线 B. ∠ACB的平分线所在的直线
C. △ABC的边BC上的中线所在的直线 D. △ABC的边AC上的高所在的直线
C
【解析】根据条件可以推出AB=AC，由此即可判断．
【解析】
∵l=AB+BC+AC，
∴BC=l?2AB=AB+BC+AC?2AB，
∴AB=AC，
∴△ABC中BC边中线所在的直线是△ABC的对称轴.
故选C. 如图，直线CD是线段AB的垂直平分线，P为直线CD上的一点，已知线段PA＝5，则线段PB的长度为（ ）
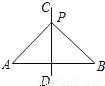
A. 6 B. 5 C. 4 D. 3
B
【解析】因为线段垂直平分线上的点与这条线段两个端点的距离相等，所以PA=PB，则PB=5.
故选B. 如图，四边形ABCD中，AC垂直平分BD，垂足为E，下列结论不一定成立的是（ ）
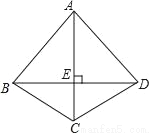
A. AB=AD B. AC平分∠BCD C. AB=BD D. △BEC≌△DEC
C
【解析】试题分析：根据AC垂直平分BD可得：△ABD为等腰三角形，即AB=AD，AC平分∠BAD，△BEC≌△DEC.