题目内容
已知△ABC的周长是l,BC=l-2AB,则下列直线一定为△ABC的对称轴的是( )
A. △ABC的边AB的垂直平分线 B. ∠ACB的平分线所在的直线
C. △ABC的边BC上的中线所在的直线 D. △ABC的边AC上的高所在的直线
C
【解析】根据条件可以推出AB=AC，由此即可判断．
【解析】
∵l=AB+BC+AC，
∴BC=l?2AB=AB+BC+AC?2AB，
∴AB=AC，
∴△ABC中BC边中线所在的直线是△ABC的对称轴.
故选C.
如图⑴～⑿中全等的图形是_____和______；_____和______；_____和______；
_____和______；_____和______；_____和______；（填图形的序号）
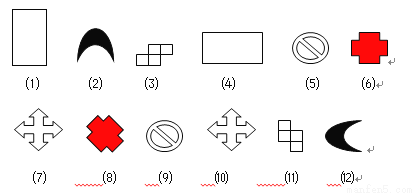
（1）、（4）；（2）、（12）；（3）、（11）；（5）、（9）；（6）、（8）；（7）、（10）
【解析】通过观察可以发现：（1）和（4）、（2）和（12）、（3）和（11）、（5）和（9）、（6）和（8）、（7）和（10）是全等形，
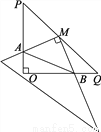
故答案为：（1）、（4）；（2）、（12）；（3）、（11）；（5）、（9）；（6）、（8）；（7）、（10）. 如图，在Rt△POQ中，OP=OQ=4，M是PQ中点，∠P=∠Q=45°，将一三角尺的直角顶点放在点M处，以M为旋转中心旋转三角尺，三角尺的两直角边与△POQ的两直角边分别交于点A、B.试说明：MA=MB.
+
说明见解析
【解析】试题分析：过点M作ME⊥PO，MF⊥QO，可得四边形OEBF是矩形，根据三角形的中位线定理可得ME=MF，再根据同角的余角相等可得再利用“角边角”证明和全等，根据全等三角形对应边相等即可证明；
试题解析：过点M作ME⊥PO，MF⊥QO，
∴∠PEM=∠QFM=90°，又∵∠P=∠Q=45°，
∴∠PME=∠QMF=45°，∠EMF=90°，
又∵P... 锐角三角形中，最大角α的取值范围是（ ）
A. 0°< α < 90° B. 60°< α < 180° C. 60°< α < 90° D. 60°≤α < 90°
D
【解析】试题分析：根据三角形的内角和定理，又α是最大角，得：3α≥180°，即α≥60°，故最大角α的取值范围是60°≤α＜180度． 如图，在△ABC中，∠B=55°，∠C=30°，分别以点A和点C为圆心，大于
AC的长为半径画弧，两弧相交于点M，N，作直线MN，交BC于点D，连接AD，则∠BAD的度数为（ ）
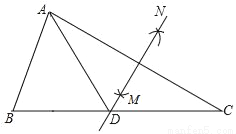
A. 65° B. 60° C. 55° D. 45°
A
【解析】分析：根据线段垂直平分线的性质得到AD=DC，根据等腰三角形的性质得到∠C=∠DAC，
求得∠DAC=30°，根据三角形的内角和得到∠BAC=95°，即可得到结论．
详解：由题意可得：MN是AC的垂直平分线，则AD=DC，故∠C=∠DAC．
∵∠C=30°，∴∠DAC=30°．
∵∠B=55°，∴∠BAC=95°，∴∠BAD=∠BAC﹣∠CAD=65°．
... 杨阳同学沿一段笔直的人行道行走,在由A步行到达B处的过程中,通过隔离带的空隙O,刚好浏览完对面人行道宣传墙上的社会主义核心价值观标语,其具体信息汇集如下:
如图,AB∥OH∥CD,相邻两平行线间的距离相等,AC,BD相交于O,OD⊥CD,垂足为D,已知AB=20米,请根据上述信息求标语CD的长度.
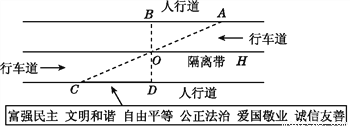
20米.
【解析】试题分析：已知AB∥CD，根据平行线的性质可得∠ABO=∠CDO，再由垂直的定义可得∠CDO=90°，可得OB⊥AB，根据相邻两平行线间的距离相等可得OD=OB，即可根据ASA定理判定△ABO≌△CDO，由全等三角形的性质即可得CD=AB=20m．
试题解析：∵AB∥CD，∴∠ABO=∠CDO，
∵OD⊥CD，∴∠CDO=90°，
∴∠ABO=90°，即O... 如图，过正方形ABCD的顶点B作直线l，过点A，C作l的垂线，垂足分别为点E，F．若AE＝2，CF＝6，则AB的长度为 ．
．
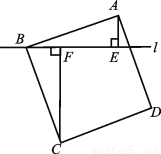
【解析】
试题分析：∵四边形ABCD是正方形，
∴∠CBF+∠FBA=90°，∠CBF+∠BCF=90°，
∴∠BCF=∠ABE，
∵∠AEB=∠BFC=90°，AB=BC，
∴△ABE≌△BCF（AAS）
∴AE=BF，BE=CF，
∴AB=．
故答案是． 超速行驶是引发交通事故的主要原因之一．上周末，小明和三位同学尝试用自己所学的知识检测车速．如图，观测点设在A处，离益阳大道的距离(AC)为30米．这时，一辆小轿车由西向东匀速行驶，测得此车从B处行驶到C处所用的时间为8秒，∠BAC＝75°.
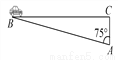
(1)求B、C两点的距离；
(2)请判断此车是否超过了益阳大道60千米/小时的限制速度？
(计算时距离精确到1米，参考数据：sin75°≈0.9659，cos75°≈0.2588，tan75°≈3.732，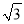 
≈1.732，60千米/小时≈16.7米/秒)
（1）112米；（2）没有超过限制速度．
【解析】【解析】
(1)在Rt△ABC中，
∠ACB＝90°，∠BAC＝75°，AC＝30，
∴BC＝AC·tan ∠BAC＝30×tan 75°≈30×3.732≈112(米)．
(2)∵此车速度＝112÷8＝14(米/秒)＜16.7(米/秒)＝60(千米/小时)
∴此车没有超过限制速度． 一个角的余角比这个角的补角小_____.
90°
【解析】设这个角是x°，由题意得
（180°- x°）-（90°- x°）=90°.