题目内容
如图，在△ABC中，∠C＝90°，D为BC上一点，且DE⊥AB于E，AC＝AE.求证：AD平分∠BAC.
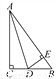
见解析
【解析】试题分析：证明Rt△ACD≌Rt△AED，利用全等三角形的性质即可得.
试题解析：∵DE⊥AB，∴∠AED=90°，
在Rt△ACD和Rt△AED中，
，
∴Rt△ACD≌Rt△AED（HL），
∴∠CAD=∠EAD，
即AD平分∠BAC.
练习册系列答案
相关题目
观察如下图所示的各个图形，其中全等图形正确的是（ ）．
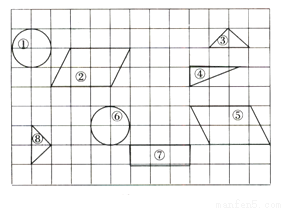
A. ②≌④ B. ⑤≌⑧ C. ①≌⑥ D. ③≌⑦
C
【解析】观察可知 ②≌⑤，③≌⑧，①≌⑥，
故选C. 如图，在四边形ABCD中，∠ADC=∠ABC=90°，AD=CD，DE⊥AB于点E，若四边形ABCD的面积为16，则DE=__.
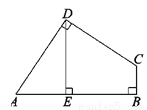
4
【解析】试题解析：过点D作BC的垂线，交BC的延长线于F，
又
∴≌，
∴，
四边形ABCD的面积=正方形DEBF的面积=16，
∴DE=4.
故答案为：4. 如图,MP,NQ分别垂直平分AB,AC,且BC=6 cm,则△APQ的周长为( )
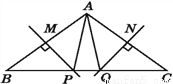
A. 12 cm B. 6 cm C. 8 cm D. 无法确定
B
【解析】由MP、NQ分别垂直平分AB、AC，根据线段垂直平分线的性质，可得BP=AP，CQ=AQ，继而求得△APQ的周长等于BC．
【解析】
∵MP、NQ分别垂直平分AB、AC，
∴BP=AP，CQ=AQ，
∵BC=6cm，
∴△APQ的周长为：AP+PQ+AQ=BP+PQ+CQ=BC=6cm.
故选B. 关于线段的垂直平分线有以下说法:
①一条线段的垂直平分线的垂足,也是这条线段的中点;
②线段的垂直平分线是一条直线;
③一条线段的垂直平分线是这条线段的唯一对称轴.
其中正确的说法有( )
A. 1个 B. 2个 C. 3个 D. 0个
B
【解析】由线段垂直平分线的定义，可得一条线段的垂直平分线的垂足，也是这条线段的中点；线段的垂直平分线是一条直线．注意举反例来判断．
【解析】
①一条线段的垂直平分线的垂足，也是这条线段的中点，正确；
②线段的垂直平分线是一条直线；正确；
③一条线段的垂直平分线是这条线段的唯一对称轴，错误，因为线段有2条对称轴：一条是这条线段的垂直平分线，另一条对称轴是这条线段所在的直... 如图，有一个直角△ABC，∠C=90°，AC=10，BC=5，一条线段PQ=AB，P.Q两点分别在AC和过点A且垂直于AC的射线AX上运动，当AP= 时,才能使ΔABC≌ΔPQA.
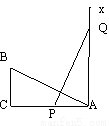
10
【解析】
试题分析：要使△ABC≌△PQA，根据全等三角形的性质可得AP=CA，则说明当P运动到C时，利用直角三角形全等的判定HL可证△ABC≌△PQA．
∵AX⊥AC，∠C=90°，
∴∠C=∠PAQ=90°，
又∵AP=CB=5，PQ=AB，
∴△ABC≌△PQA．
点P运动到C点时，△ABC≌△PQA．
∵AX⊥AC，∠C=90°，
... 如图，在直角坐标系内，O为原点，点A的坐标为(10，0)，点B在第一象限内，BO＝5，sin∠BOA＝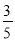
. 求：(1)点B的坐标；(2)cos∠BAO的值．
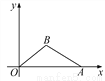
（1）点B的坐标为(4，3)；（2）cos∠BAO＝.
【解析】试题分析：（1）作BH⊥OA， 垂足为H，在Rt△OHB中，根据锐角三角函数的定义及已知条件求得BH的长，再根据勾股定理求得OH的长，即可得点B的坐标；（2）先求得AH的长，在Rt△AHB中，根据勾股定理求得AB的长，根据锐角三角函数的定义即可求得cos∠BAO的值．
试题解析：
(1)如图所示，作BH⊥OA， 垂足... 在△ABC中，AB=AC，AB的垂直平分线DE与AC所在的直线相交于点E，垂足为D，连接BE．已知AE=5，tan∠AED=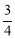
，则BE+CE= ．
6或16
【解析】
试题分析：有两种情形，需要分类讨论：
①若∠BAC为锐角，如答图1所示，
∵AB的垂直平分线是DE，∴AE=BE，ED⊥AB，AD=AB。
∵AE=5，tan∠AED=，∴sin∠AED=。
∴AD=AE•sin∠AED=3。∴AB=6。
∴BE+CE=AE+CE=AC=AB=6。
②若∠BAC为钝角，如答图2所示，同理可求得：B... 设直线l1和直线l2平行，且l1和l2间的距离为a．如果线段AB在l1的右侧，并设AB关于l1的对称图形是A′B′，而A′B′关于l2的对称图形是A″B″（如图），那么，线段AB和A″B″有什么关系？
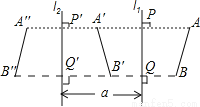
A''B''平行且等于AB，理由见解析
【解析】试题分析：根据轴对称的性质，及在平面内垂直于同一条直线的两条直线互相平行，即可判断ABB''A''为平行四边形，继而得出答案．
试题解析：【解析】
因为l1平行于l2，并且AA″垂直于l1，当然也垂直于l2，同理BB″也垂直于l1和l2．
又在平面内垂直于同一条直线的两条直线互相平行，
所以AA″∥BB″①
另一方面，...