题目内容
如图,△ABC,△CDE均为等腰直角三角形,∠ACB=∠DCE=90°,点E在AB上,试说明:△CDA≌△CEB.
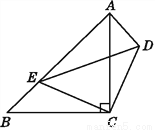
答案见解析
【解析】试题分析：根据等腰直角三角形的性质得出CE=CD，BC=AC，再利用全等三角形的判定证明即可．
试题解析：证明：∵△ABC、△CDE均为等腰直角三角形，∠ACB=∠DCE=90°，
∴CE=CD，BC=AC，
∴∠ACB﹣∠ACE=∠DCE﹣∠ACE，
∴∠ECB=∠DCA，
在△CDA与△CEB中， ，
∴△CDA≌△CEB．
练习册系列答案
相关题目
对于图形的全等，下列叙述不正确的是（ ）
A. 一个图形经过旋转后得到的图形，与原来的图形全等
B. 一个图形经过中心对称后得到的图形，与原来的图形全等
C. 一个图形放大后得到的图形，与原来的图形全等
D. 一个图形经过轴对称后得到的图形，与原来的图形全等
C
【解析】A. 一个图形经过旋转后得到的图形，与原来的图形全等，正确，不符合题意；
B. 一个图形经过中心对称后得到的图形，与原来的图形全等，正确，不符合题意；
C. 一个图形放大后得到的图形，与原来的图形不全等，故错误，符合题意；
D. 一个图形经过轴对称后得到的图形，与原来的图形全等，正确，不符合题意，
故选C. 长为l的一根绳，恰好可围成两个全等三角形，则其中一个三角形的最长边x的取值范围为__________.
≤x＜
【解析】试题解析：∵围成两个全等的三角形可得两个三角形的周长相等，
∴可得
又因为x为最长边大于周长的，
综上可得
故答案为： 如图，在△ABC中，∠B=55°，∠C=30°，分别以点A和点C为圆心，大于
AC的长为半径画弧，两弧相交于点M，N，作直线MN，交BC于点D，连接AD，则∠BAD的度数为（ ）
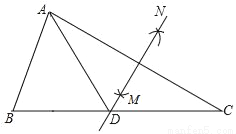
A. 65° B. 60° C. 55° D. 45°
A
【解析】分析：根据线段垂直平分线的性质得到AD=DC，根据等腰三角形的性质得到∠C=∠DAC，
求得∠DAC=30°，根据三角形的内角和得到∠BAC=95°，即可得到结论．
详解：由题意可得：MN是AC的垂直平分线，则AD=DC，故∠C=∠DAC．
∵∠C=30°，∴∠DAC=30°．
∵∠B=55°，∴∠BAC=95°，∴∠BAD=∠BAC﹣∠CAD=65°．
... 下列说法中:
①P是线段AB上的一点,直线l经过点P且l⊥AB,则l是线段AB的垂直平分线;
②直线l经过线段AB的中点,则l是线段AB的垂直平分线;
③若AP=PB,且直线l垂直于线段AB,则l是线段AB的垂直平分线;
④经过线段AB的中点P且垂直于AB的直线l是线段AB的垂直平分线.
其中正确的有( )
A. 1个 B. 2个 C. 3个 D. 4个
A
【解析】根据线段的垂直平分线的定义，以及定理：到线段的两端距离相等的点在线段的垂直平分线上，即可判断．
【解析】
①当P不是AB的中点，则直线l不平分线段AB，故错误；
②直线l经过线段AB的中点，且垂直于AB则l是线段AB的垂直平分线，故错误；
③若AP=PB，则P在线段AB的垂直平分线上，但l不一定过点P，所以直线l不一定是线段AB的垂直平分线，故错误；
④... 如图，过正方形ABCD的顶点B作直线l，过点A，C作l的垂线，垂足分别为点E，F．若AE＝2，CF＝6，则AB的长度为 ．
．
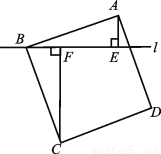
【解析】
试题分析：∵四边形ABCD是正方形，
∴∠CBF+∠FBA=90°，∠CBF+∠BCF=90°，
∴∠BCF=∠ABE，
∵∠AEB=∠BFC=90°，AB=BC，
∴△ABE≌△BCF（AAS）
∴AE=BF，BE=CF，
∴AB=．
故答案是． 在△ABC中，∠C＝90°，cosA＝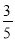
，AC＝6.求△ABC的周长和面积．
周长为24，面积为24.
【解析】试题分析：根据余弦的定义求出斜边AB的长，再根据勾股定理求出BC的长，再根据三角形的周长、面积的求法即可得.
试题解析：∵∠C=90°，∴cosA=，
∵cosA＝，AC＝6，
∴AB=10，
∴BC==8，
∴△ABC的周长=AC+BC+AB=6+8+10=24，
S△ABC==24. 将一副三角尺如图所示叠放在一起，则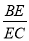
的值是 ．
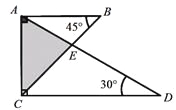
【解析】试题分析：设AC=BC=x，则CD= ，证得AB∥CD，进而得△ABE∽△DCE，所以=．
故答案为： . 如图，l是线段AB的对称轴，l′是线段BC的对称轴，l和l′相交于点O．OA与OC相等吗？为什么？
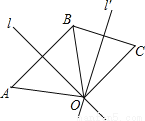
相等，理由见解析
【解析】试题分析：由轴对称的性质即可证明．
试题解析：【解析】
∵l是线段AB的对称轴，∴OA=OB，
∵l′是线段BC的对称轴，∴OB=OC，
∴OA=OC．